题目内容
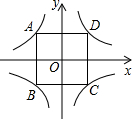 在同一平面直角坐标系中,反比例函数y=
在同一平面直角坐标系中,反比例函数y=| k |
| x |
| k |
| x |
应用:若点P(1,-
| 3 |
探究:试求“美丽四曲线8”的“伴随正方形”的面积.
考点:反比例函数图象上点的坐标特征,反比例函数系数k的几何意义
专题:新定义
分析:根据题意及反比例函数的性质,将(1,-
)代入y=-
即可得到n的值,根据反比例函数的对称性求及反比例函数的k的几何意义求出AEOH的面积即可解答.
| 3 |
| n |
| x |
解答:解:将(1,-
)代入y=-
得,-
=-
,
解得n=
;
如图:根据反比例函数的对称性可知:AE=AH,
则四边形AEOH为正方形,
其面积为
,
伴随正方形的面积为
×4=4
.
| 3 |
| n |
| x |
| 3 |
| n |
| 1 |

解得n=
| 3 |
如图:根据反比例函数的对称性可知:AE=AH,
则四边形AEOH为正方形,
其面积为
| 3 |
伴随正方形的面积为
| 3 |
| 3 |
点评:本题考查了关于反比例函数的新定义,要熟悉反比例函数图象上点的坐标特征和k的几何意义.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
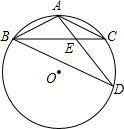 如图,A、B、C、D是圆O上的四个点,AB=AC,AD交BC于点E,AE=3,AD=7,则AB的长为( )
如图,A、B、C、D是圆O上的四个点,AB=AC,AD交BC于点E,AE=3,AD=7,则AB的长为( )| A、3 | ||
B、2
| ||
C、
| ||
D、3
|
二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
(1)ac<0;
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| x | … | 0 | 1 | 2 | … |
| y | … | -4 | -4 | 0 | … |
(2)当x>1时,y的值随x值得增大而增大;
(3)-1是方程ax2+bx+c=0的一个根;
(4)当-1<x<2时,ax2+bx+c<0
其中正确的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
多项式9a2x2-18a3x3-36a4x4各项的公因式是( )
| A、a2x2 |
| B、a3x3 |
| C、9a2x2 |
| D、9a4x4 |
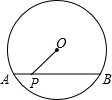 如图,⊙O的直径为10,弦AB的长是8,P是AB上的一个动点,则
如图,⊙O的直径为10,弦AB的长是8,P是AB上的一个动点,则