题目内容
16. 如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A、B两点,它们的横坐标分别为1和5.
如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A、B两点,它们的横坐标分别为1和5.(1)当m=5时,求直线AB的解析式及△AOB的面积;
(2)当y1>y2时,直接写出x的取值范围.
分析 (1)根据待定系数法即可求得直线AB的解析式,然后求得直线与x轴的交点,根据三角形面积公式求得即可.
(2)根据图象求得即可.
解答  解:(1)①当m=5时,
解:(1)①当m=5时,
∴A(1,5),B(5,1),
设y=kx+b,代入A(1,5),B(5,1)得:$\left\{\begin{array}{l}{k+b=5}\\{5k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$
∴y=-x+6;
②设直线AB与x轴交点为M,
∴M(6,0),
∴SAOB=S△AOM-S△MOB=$\frac{1}{2}$×6×5-$\frac{1}{2}$×6×1=12;
(2)由图象可知:1<x<5或x<0.
点评 本题考查了反比例函数与一次函数的交点的应用,能读懂图象是解此题的关键,注意:数形结合思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.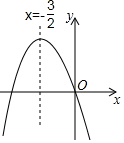 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正确的结论有( )
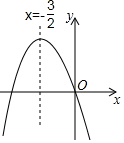 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.点M(-3,2)关于y轴对称的点的坐标为( )
| A. | (-3,-2) | B. | (3,-2) | C. | (-3,2) | D. | (3,2) |
 如图,四边形OABC是矩形,ADEF是边长为2的正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=$\frac{6}{x}$的图象上,则AB的长为6.
如图,四边形OABC是矩形,ADEF是边长为2的正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=$\frac{6}{x}$的图象上,则AB的长为6.