题目内容
4.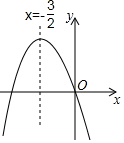 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线开口方向得到a<0以及函数经过原点即可判断①,由抛物线的对称轴方程得到为b=2a<0,以及a的符号即可判断③;根据x=1时的函数值可以判断②;根据抛物线与x轴交点个数得到△=b2-4ac>0,则可对④进行判断.
解答 解:∵抛物线开口向下,
∴a<0,
∵抛物线经过原点,
∴c=0,
则abc=0,所以①正确;
当x=1时,函数值是a+b+c<0,则②错误;
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=-$\frac{3}{2}$<0,
∴b=3a<0,
又∵a<0,
∴a>b,则③正确;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以④错误.
故选B.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
15.参加学校科普知识竞赛决赛的5名同学A,B,C,D,E在赛后知道了自己的成绩,想尽快得知比赛的名次,大家互相打听后得到了以下消息:(分别以相应字母来对应他们本人的成绩)
(1)请参照表中第二条文字信息的翻译方式,在表中写出其它三条文字信息的数学表达式;
(2)5位同学的比赛名次依次是B>D>E>C>A.(仿照第二条信息的数学表达式用“>”连接)
| 信息序号 | 文字信息 | 数学表达式 |
| 1 | C和D的得分之和是E得分的2倍 | C+D=2E |
| 2 | B的得分高于D | B>D |
| 3 | A和B的得分之和等于C和D的总分 | A+B=C+D |
| 4 | D的得分高于E | D>E |
(2)5位同学的比赛名次依次是B>D>E>C>A.(仿照第二条信息的数学表达式用“>”连接)
9.在△ABC和△A'B'C'中,已知∠A=∠A′,∠B=∠B',AB=A'B',那么△ABC≌△A′B′C′运用的判定方法是( )
| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
13.下列命题中,真命题的个数是( )
①经过三点一定可以作圆;
②一个正五边形只有一个外接圆和一个内切圆;
③正多边形半径的长就是正多边形的中心到顶点的距离;
④三角形的外心到三角形的三个顶点距离相等.
①经过三点一定可以作圆;
②一个正五边形只有一个外接圆和一个内切圆;
③正多边形半径的长就是正多边形的中心到顶点的距离;
④三角形的外心到三角形的三个顶点距离相等.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.若二次函数y=ax2+b的图象经过点P(-2,4),则下列各点中,一定在该图象上的是( )
| A. | (-4,2) | B. | (4,-2) | C. | (2,4) | D. | (-2,-4) |
 如图,⊙M与x轴交于A、B两点,与y轴切于点C,且OA,OB的长是方程x2-4x+3=0的解.
如图,⊙M与x轴交于A、B两点,与y轴切于点C,且OA,OB的长是方程x2-4x+3=0的解. 如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A、B两点,它们的横坐标分别为1和5.
如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A、B两点,它们的横坐标分别为1和5.