题目内容
7.计算:4sin30°-$\sqrt{2}$cos45°+tan60°=1+$\sqrt{3}$.分析 根据特殊角三角函数值,可得答案.
解答 解:原式=4×$\frac{1}{2}$-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+$\sqrt{3}$=$1+\sqrt{3}$,
故答案为:1+$\sqrt{3}$.
点评 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.

练习册系列答案
相关题目
12.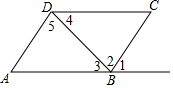 如图,由AD∥BC可以得到的结论是( )
如图,由AD∥BC可以得到的结论是( )
 如图,由AD∥BC可以得到的结论是( )
如图,由AD∥BC可以得到的结论是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠2=∠5 | D. | ∠3=∠4 |
17.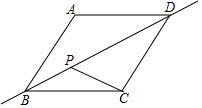 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )| A. | $\frac{4}{3}\sqrt{3}$ | B. | $\frac{2}{3}\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
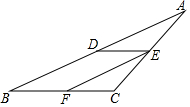 如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?
如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?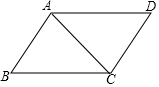 如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.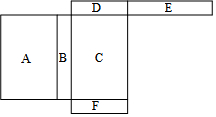 如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题.
如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题. 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).
如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).