题目内容
16.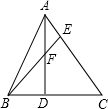 如图,△ABC中,D、E是BC、AC上的点,AD、BE交于F,若已知BD:DC=2:3,AE:EC=1:3.
如图,△ABC中,D、E是BC、AC上的点,AD、BE交于F,若已知BD:DC=2:3,AE:EC=1:3.(1)AF:FD;
(2)BF:FE.
分析 (1)首先作DG∥AC,交BE于点G,根据BD:DC=2:3,可得BD:BC=2:5;然后根据DG∥AC,AE:EC=1:3,求出$\frac{DG}{AE}$的值是多少,即可求出AF:FD的值是多少.
(2)首先作EH∥BC,交AD于点H,根据AE:EC=1:3,可得AE:AC=1:4;然后根据EH∥BC,BD:DC=2:3,求出$\frac{EH}{BD}$的值是多少,即可求出BF:FE的值是多少.
解答 解:(1)如图1,作DG∥AC,交BE于点G,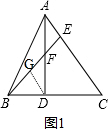
∵BD:DC=2:3,
∴BD:BC=2:5,
∵DG∥AC,
∴$\frac{DG}{EC}=\frac{BD}{BC}=\frac{2}{5}$,
又∵AE:EC=1:3,
∴$\frac{DG}{3AE}=\frac{2}{5}$,
∴$\frac{DG}{AE}$=$\frac{6}{5}$,
∴$\frac{AF}{FD}=\frac{AE}{DG}=\frac{5}{6}$,
即AF:FD=5:6.
(2)如图2,作EH∥BC,交AD于点H,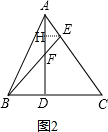
∵AE:EC=1:3,
∴AE:AC=1:4,
∵EH∥BC,
∴$\frac{EH}{CD}=\frac{AE}{AC}=\frac{1}{4}$,
又∵BD:DC=2:3,
∴$\frac{EH}{\frac{3}{2}BD}=\frac{1}{4}$,
∴$\frac{EH}{BD}=\frac{3}{8}$,
∴$\frac{BF}{FE}=\frac{BD}{HE}=\frac{8}{3}$,
即BF:FE=8:3.
点评 此题主要考查了平行线分线段成比例问题,要熟练掌握,解答此题的关键是要明确:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
相关题目
11.电视台“市民热线”对上个月内接到的热线电话进行了分类统计,不分数据如表:
根据已有信息,解答下列问题:
(1)讲表格补充完整;
(2)在扇形统计图中,各类数据对应的圆心角分别是多少度?
(3)画出扇形统计图,标上各类型相应的百分比,并写上统计图的名称.
| 类型 | 个数 | 百分比 |
| 城建 | 30 | 10% |
| 环保 | 180 | 60% |
| 道路交通 | 60 | 20% |
| 其他方面 | 30 | 10% |
(1)讲表格补充完整;
(2)在扇形统计图中,各类数据对应的圆心角分别是多少度?
(3)画出扇形统计图,标上各类型相应的百分比,并写上统计图的名称.
 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H. 已知:如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点.求证:△ABM≌△DCM.
已知:如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点.求证:△ABM≌△DCM.