题目内容
5. 已知:如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点.求证:△ABM≌△DCM.
已知:如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点.求证:△ABM≌△DCM.
分析 先根据等腰三角形的性质得出AB=DC,∠A=∠D,再由M是AD的中点得出AM=DM,根据SAS定理即可得出结论.
解答 证明:∵形ABCD是等腰梯形,AD∥BC,
∴AB=CD,∠A=∠D.
又∵M是AD的中点,
∴AM=DM.
在△ABM与△DCM中,
∵$\left\{\begin{array}{l}AB=DC\\∠A=∠D\\ AM=DM\end{array}\right.$,
∴△ABM≌△DCM.
点评 本题考查的是等腰三角形的性质,熟知等腰梯形同一底上的两个角相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.将直线y=x-1平移,使得它经过点(-2,0),则平移后的直线为( )
| A. | y=x-2 | B. | y=x+1 | C. | y=-x-2 | D. | y=x+2 |
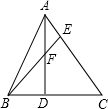 如图,△ABC中,D、E是BC、AC上的点,AD、BE交于F,若已知BD:DC=2:3,AE:EC=1:3.
如图,△ABC中,D、E是BC、AC上的点,AD、BE交于F,若已知BD:DC=2:3,AE:EC=1:3.