题目内容
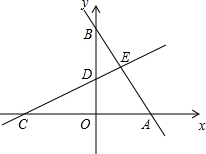 在平面直角坐标系中,函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,折叠线段AB,使点A、B重合,折痕分别交线段AB、y轴、x轴于点E、D、C.求直线CE的函数解析式.
在平面直角坐标系中,函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,折叠线段AB,使点A、B重合,折痕分别交线段AB、y轴、x轴于点E、D、C.求直线CE的函数解析式.考点:一次函数综合题
专题:
分析:根据函数y=-2x+8求得A、B的坐标,进而求得E的坐标,然后根据三角形相似求得C的坐标,最后根据待定系数法即可求得直线CE的函数解析式.
解答:解:∵函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,
∴A(4,0),B(0,8),
∴OA=4,OB=8,
∴AB=
=4
∵折叠线段AB,使点A、B重合,
∴E是AB的中点,
∴E(2,4),AE=
AB=2
,
∵折叠线段AB,使点A、B重合,折痕为CE,
∴CE⊥AB,
∴∠AEC=∠AOB=90°,
∵∠OAB=∠EAC,
∴△AOB∽△AEC,
∴
=
,即
=
,
∴AC=10,
∴OC=AC-OA=6,
∴C(-6,0).
设直线CE解析式为y=kx+b,
∴
,
解得
,
∴直线CE解析式为y=
x+3.
∴A(4,0),B(0,8),
∴OA=4,OB=8,
∴AB=
| 42+82 |
| 5 |
∵折叠线段AB,使点A、B重合,
∴E是AB的中点,
∴E(2,4),AE=
| 1 |
| 2 |
| 5 |
∵折叠线段AB,使点A、B重合,折痕为CE,
∴CE⊥AB,
∴∠AEC=∠AOB=90°,
∵∠OAB=∠EAC,
∴△AOB∽△AEC,
∴
| AC |
| AB |
| AE |
| OA |
| AC | ||
4
|
2
| ||
| 4 |
∴AC=10,
∴OC=AC-OA=6,
∴C(-6,0).
设直线CE解析式为y=kx+b,
∴
|
解得
|
∴直线CE解析式为y=
| 1 |
| 2 |
点评:本题是一次函数的综合题,考查了一次函数图象上点的坐标特征,勾股定理的应用,三角形相似的判定和性质,以及待定系数法的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在△ABC中,AB=AC,CD⊥AB于D,则下列判断正确的是( )
如图,在△ABC中,AB=AC,CD⊥AB于D,则下列判断正确的是( )| A、∠A=∠B |
| B、∠A=∠ACD |
| C、∠A=∠DCB |
| D、∠A=2∠BCD |
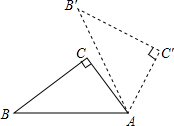 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )| A、π | ||
B、
| ||
C、
| ||
D、
|
有一块长方形黑板,长为120cm,对角线长为150cm,则它的宽为( )
| A、76cm | B、90cm |
| C、80cm | D、60cm |
将y=3x2的图象向右平移1个单位,再向上平移3个单位,得到的抛物线的解析式为( )
| A、y=3(x-1)2-3 |
| B、y=3(x+1)2+3 |
| C、y=3(x+1)2-3 |
| D、y=3(x-1)2+3 |
在0,-
,
,0.1010010001…,
这五个数中,是无理数的有( )个.
| 1 |
| 3 |
| 9 |
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
 如图,若∠1=∠4,则AB∥CD,若∠2=∠3,则AD∥BC,以上判断所依据的定理是
如图,若∠1=∠4,则AB∥CD,若∠2=∠3,则AD∥BC,以上判断所依据的定理是 已知,如图,在△ABC中,AB=8,BC=20,BC边上的中线AD=6,则△ADC的面积
已知,如图,在△ABC中,AB=8,BC=20,BC边上的中线AD=6,则△ADC的面积