题目内容
 如图,在△ABC中,AB=AC,CD⊥AB于D,则下列判断正确的是( )
如图,在△ABC中,AB=AC,CD⊥AB于D,则下列判断正确的是( )| A、∠A=∠B |
| B、∠A=∠ACD |
| C、∠A=∠DCB |
| D、∠A=2∠BCD |
考点:等腰三角形的性质
专题:
分析:根据等腰三角形的性质可知∠B=∠ACB=
(180°-∠A),再根据直角三角形两锐角互余可得到答案.
| 1 |
| 2 |
解答:解:∵AB=AC,
∴∠B=∠ACB,
又CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠A+∠ACD=∠B+∠BCD,
又∠ACD=∠ACB-∠BCD,
∴∠A+∠B-∠BCD=∠B+∠BCD,
∴∠A=2∠BCD,
故选D.
∴∠B=∠ACB,
又CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠A+∠ACD=∠B+∠BCD,
又∠ACD=∠ACB-∠BCD,
∴∠A+∠B-∠BCD=∠B+∠BCD,
∴∠A=2∠BCD,
故选D.
点评:本题主要考查等腰三角形的性质,掌握等腰三角形的两底角相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 从正面看和左面看由若干个完全相同的小立方体组成的一个几何体所得到的图形如图所示,则搭成这几个几何体的小立方块的块数可能是( )
从正面看和左面看由若干个完全相同的小立方体组成的一个几何体所得到的图形如图所示,则搭成这几个几何体的小立方块的块数可能是( )| A、5块或6块 |
| B、4块或5块 |
| C、3块或4块或5块 |
| D、6块或7块 |
某商场将某种商品按原价的8折出售,此时商品的利润率是10%,已知这种商品的进价为1600元,则该商品的原价为每件( )
| A、2200元 |
| B、2280元 |
| C、1840元 |
| D、1760元 |
 如图所示是用铁丝围成的一个梯形,将其改成一个长和宽比为2:1的长方形,那么长方形的长和宽分别为多少?
如图所示是用铁丝围成的一个梯形,将其改成一个长和宽比为2:1的长方形,那么长方形的长和宽分别为多少? 如图,已知线段AB=2,延长线段AB到C,使BC=2AB,点D是线段AC的中点,则DC的长等于
如图,已知线段AB=2,延长线段AB到C,使BC=2AB,点D是线段AC的中点,则DC的长等于 如图,线段AB=8,C是线段AB的中点,点D在CB上,DB=1.5,求线段CD的长.
如图,线段AB=8,C是线段AB的中点,点D在CB上,DB=1.5,求线段CD的长.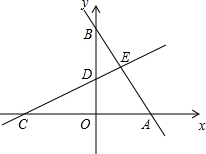 在平面直角坐标系中,函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,折叠线段AB,使点A、B重合,折痕分别交线段AB、y轴、x轴于点E、D、C.求直线CE的函数解析式.
在平面直角坐标系中,函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,折叠线段AB,使点A、B重合,折痕分别交线段AB、y轴、x轴于点E、D、C.求直线CE的函数解析式.