题目内容
 已知,如图,在△ABC中,AB=8,BC=20,BC边上的中线AD=6,则△ADC的面积
已知,如图,在△ABC中,AB=8,BC=20,BC边上的中线AD=6,则△ADC的面积考点:全等三角形的判定与性质,勾股定理的逆定理
专题:
分析:由BC=20,BC边上的中线AD=6,可得BD=CD=10,过A点作AE⊥BC,垂足为点E,由三角形的面积公式可得:△ADC的面积=
•DC•AE=
•BD•AE=△ABD的面积,由因为在△ABD中,AB=8,AD=6,BD=10,可得△ABD为直角三角形,然后根据直角三角形的面积公式计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:过A点作AE⊥BC,垂足为点E,

∵AD是BC边上的中线,BC=20,
∴BD=CD=
BC=
•20=10,
在△ABD中,AB=8,BD=10,AD=6,
∵AB2+AD2=82+62=100=102=BD2,
∴△ABD是直角三角形,且∠BAD=90°,
∴△ABD的面积=
•AB•AD=
×8×6=24,
∵△ADC的面积=
•DC•AE=
•BD•AE=△ABD的面积,
∴△ADC的面积=24.
故答案为:24.

∵AD是BC边上的中线,BC=20,
∴BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABD中,AB=8,BD=10,AD=6,
∵AB2+AD2=82+62=100=102=BD2,
∴△ABD是直角三角形,且∠BAD=90°,
∴△ABD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ADC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ADC的面积=24.
故答案为:24.
点评:此题考查了三角形的面积计算,解题的关键是:将△ADC的面积转化为△ABD的面积.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、3a3+2a2=5a6 | ||||||
B、3
| ||||||
| C、a4•a2=a8 | ||||||
| D、3(a2)3=3a5 |
估计
的值是( )
| 8 |
| A、在1和2之间 |
| B、在2和3之间 |
| C、在3和4之间 |
| D、在5和6之间 |
 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,⊙O的切线AP与OC的延长线相交于点P,若PO=6cm,求AC的长.
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,⊙O的切线AP与OC的延长线相交于点P,若PO=6cm,求AC的长. 如图,已知线段AB=2,延长线段AB到C,使BC=2AB,点D是线段AC的中点,则DC的长等于
如图,已知线段AB=2,延长线段AB到C,使BC=2AB,点D是线段AC的中点,则DC的长等于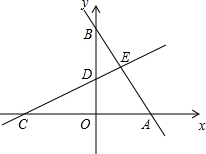 在平面直角坐标系中,函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,折叠线段AB,使点A、B重合,折痕分别交线段AB、y轴、x轴于点E、D、C.求直线CE的函数解析式.
在平面直角坐标系中,函数y=-2x+8的图象分别是交x轴、y轴于A、B两点,折叠线段AB,使点A、B重合,折痕分别交线段AB、y轴、x轴于点E、D、C.求直线CE的函数解析式.