Question

9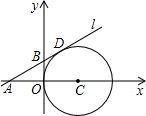．如图，在平面直角坐标系中，⊙C与y轴相切，且C点坐标为（2，0），直线l过点A（-2，0），与⊙C相切于点D，求直线l的解析式．

Answer 1

分析 连接CD，由于直线l为⊙C的切线，故CD⊥AD．结合点与坐标的性质求得点B的坐标，设直线l的函数解析式为y=kx+b，把A，B两点的坐标代入即可求出未知数的值从而求出其解析式．

解答 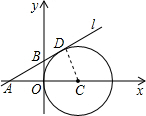解：如图所示，当直线l在x轴的上方时，
连接CD，
∵直线l为⊙C的切线，
∴CD⊥AD．
∵C点坐标为（2，0），
∴OC=2，即⊙C的半径为2，
∴CD=OC=2．
又∵点A的坐标为（-2，0），
∴AC=4，
∴AC=2CD，
∴∠CAD=30°，
在Rt△AOB中，OB=OA•tan30°=$\frac{2\sqrt{3}}{3}$，
即B（0，$\frac{2\sqrt{3}}{3}$），
设直线l解析式为：y=kx+b（k≠0），则 $\left\{\begin{array}{l}{-2k+b=0}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$，
解得k=$\frac{\sqrt{3}}{3}$，b=$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$，
∴直线l的函数解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$．
同理可得，当直线l在x轴的下方时，直线l的函数解析式为y=-$\frac{\sqrt{3}}{3}$x-$\frac{2\sqrt{3}}{3}$．
故直线l的函数解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$或y=-$\frac{\sqrt{3}}{3}$x-$\frac{2\sqrt{3}}{3}$．

点评 本题把求一次函数的解析式与圆的性质相结合，增加了题目的难度，解答此题的关键是作出辅助线，构造出直角三角形，利用解直角三角形的知识解答．