题目内容
5. 四边形ABCD为矩形,H、F为AD、BC中点,BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线,证明EFGH为矩形.
四边形ABCD为矩形,H、F为AD、BC中点,BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线,证明EFGH为矩形.
分析 由矩形的性质和已知条件证出四边形AFCH、四边形BFDH是平行四边形,得出AF∥HC,BH∥FD,证出四边形EFGH是平行四边形,再由角平分线证出∠HEF=∠AEB=90°,即可得出四边形EFGH为矩形.
解答 证明:∵四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,AD=BC,AD∥BC,
∵H、F为AD、BC中点,
∴AH=DH=$\frac{1}{2}$AD,BF=CF=$\frac{1}{2}$BC,
∴AH=DH=BF=CF,
∴四边形AFCH、四边形BFDH是平行四边形,
∴AF∥HC,BH∥FD,
∴四边形EFGH是平行四边形,
又∵BH、AF是∠ABC、∠BAD的角平分线,
∴∠ABH=45°,∠BAF=45°,
∴∠HEF=∠AEB=90°,
∴四边形EFGH为矩形.
点评 本题考查了矩形的性质与判定、平行四边形的判定与性质;熟练掌握矩形的性质,证明四边形为平行四边形是解决问题的关键.

练习册系列答案
相关题目
16.$\root{3}{-8}$等于( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |
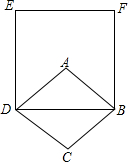 如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.
如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.