题目内容
17.计算:(1)1+2+3+4+5+…+2005+2006;
(2)(1-$\frac{1}{1004}$)(1-$\frac{1}{1005}$)(1-$\frac{1}{1006}$)(1-$\frac{1}{1007}$)…(1-$\frac{1}{2005}$)(1-$\frac{1}{2006}$)
分析 (1)根据等差数列求和公式即可求解;
(2)先计算小括号里面的减法,再约分计算即可求解.
解答 解:(1)1+2+3+4+5+…+2005+2006
=(1+2006)×2006÷2
=2007×2006÷2
=2013021;
(2)(1-$\frac{1}{1004}$)(1-$\frac{1}{1005}$)(1-$\frac{1}{1006}$)(1-$\frac{1}{1007}$)…(1-$\frac{1}{2005}$)(1-$\frac{1}{2006}$)
=$\frac{1003}{1004}$×$\frac{1004}{1005}$×…×$\frac{2005}{2006}$
=$\frac{1003}{2006}$
=$\frac{1}{2}$.
点评 本题考查的是有理数的运算能力.注意:要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;注意灵活运用运算定律简便计算.

练习册系列答案
相关题目
8.某商店老板销售一种商品,他要以不低于进价20%的利润才能出售,但为了获得更多的利润,他以高出进价80%的价格标价,若你想买下标价为360元的这种商品,商店老板让价的最大限度为( )
| A. | 82元 | B. | 100元 | C. | 120元 | D. | 160元 |
 四边形ABCD为矩形,H、F为AD、BC中点,BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线,证明EFGH为矩形.
四边形ABCD为矩形,H、F为AD、BC中点,BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线,证明EFGH为矩形.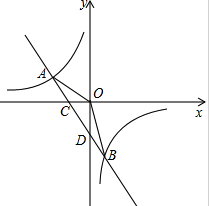 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,点A的坐标为(-2,1),点B的坐标为($\frac{1}{2}$,m).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,点A的坐标为(-2,1),点B的坐标为($\frac{1}{2}$,m). 如图,在△ABC中,BC=10,cosC=$\frac{1}{8}$,AC=8,求∠B的正切值.
如图,在△ABC中,BC=10,cosC=$\frac{1}{8}$,AC=8,求∠B的正切值. B.
B.  C.
C.  D.
D. 