题目内容
18.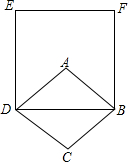 如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.
如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.
分析 连接AC交BD于点O,得出△ABC是等边三角形,利用菱形的性质和勾股定理求得BO,得出BD,即可利用正方形的面积解决问题.
解答 解:如图,
连接AC交BD于点O,
∵在菱形ABCD中,∠ABC=60°,AB=BC,AB=4,
∴△ABC是等边三角形∠ABO=30°,AO=2,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=2$\sqrt{3}$,
∴BD=4$\sqrt{3}$,
∴正方形BDEF的面积为48.
故答案为:48.
点评 此题考查菱形的性质,勾股定理,等边三角形的判定与性质,注意特殊角的运用是解决问题的关键.

练习册系列答案
相关题目
6.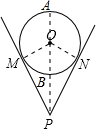 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )| A. | $\frac{50}{3}$πcm | B. | 50πcm | C. | $\frac{50}{6}$πcm | D. | 50$\sqrt{3}$πcm |
13. 如图是一个立体图形及其主视图,则它的俯视图是( )
如图是一个立体图形及其主视图,则它的俯视图是( )
 如图是一个立体图形及其主视图,则它的俯视图是( )
如图是一个立体图形及其主视图,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
3.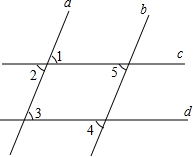 如图所示,则下列说法中不正确的是( )
如图所示,则下列说法中不正确的是( )
 如图所示,则下列说法中不正确的是( )
如图所示,则下列说法中不正确的是( )| A. | 由a∥b能得到∠2=∠5 | B. | 由c∥d能得到∠3=∠1 | ||
| C. | 由c∥d能得到∠3=∠4 | D. | 由a∥b能得到∠1=∠5 |
8.某商店老板销售一种商品,他要以不低于进价20%的利润才能出售,但为了获得更多的利润,他以高出进价80%的价格标价,若你想买下标价为360元的这种商品,商店老板让价的最大限度为( )
| A. | 82元 | B. | 100元 | C. | 120元 | D. | 160元 |
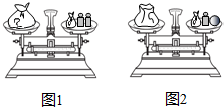 如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各10克的砝码,将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,现从图2右侧盘中拿掉砝码和袋子外面的玻璃球,只剩下一小袋玻璃球,要使天平保持平衡,则左侧袋中需拿出玻璃球的个数为( )
如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各10克的砝码,将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,现从图2右侧盘中拿掉砝码和袋子外面的玻璃球,只剩下一小袋玻璃球,要使天平保持平衡,则左侧袋中需拿出玻璃球的个数为( )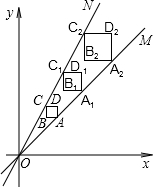 如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.
如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.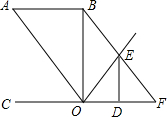 如图,已知AB∥CF,O为直线CF上一点,且OB平分∠AOE,ED⊥CF于D,且∠OBF=∠OED,∠BFC=∠A,那么OB和CF有怎样的位置关系?为什么?
如图,已知AB∥CF,O为直线CF上一点,且OB平分∠AOE,ED⊥CF于D,且∠OBF=∠OED,∠BFC=∠A,那么OB和CF有怎样的位置关系?为什么? 四边形ABCD为矩形,H、F为AD、BC中点,BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线,证明EFGH为矩形.
四边形ABCD为矩形,H、F为AD、BC中点,BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线,证明EFGH为矩形.