题目内容
14．已知$\frac{a-b}{x}$=$\frac{b-c}{y}$=$\frac{c-a}{z}$≠0，求x+y+z的值．分析 设$\frac{a-b}{x}$=$\frac{b-c}{y}$=$\frac{c-a}{z}$=k，根据比例的性质表示出x、y、z，代入计算即可得到答案．
解答 解：设$\frac{a-b}{x}$=$\frac{b-c}{y}$=$\frac{c-a}{z}$=k，
则x=ka-kb，y=kb-kc，z=kc-ka，
x+y+z
=ka-kb+kb-kc+kc-ka
=0．
点评 本题考查的是比例的性质，正确设出参数、灵活运用比例的性质是解题的关键．
练习册系列答案
相关题目
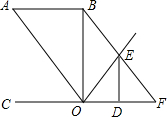如图，已知AB∥CF，O为直线CF上一点，且OB平分∠AOE，ED⊥CF于D，且∠OBF=∠OED，∠BFC=∠A，那么OB和CF有怎样的位置关系？为什么？
四边形ABCD为矩形，H、F为AD、BC中点，BH、AF、DF、CH是∠B、∠A、∠D、∠C的角平分线，证明EFGH为矩形．
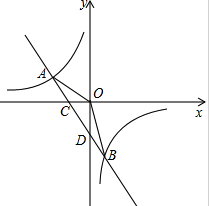如图，一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，与x轴交于点C，与y轴交于点D，点A的坐标为（-2，1），点B的坐标为（$\frac{1}{2}$，m）．
如图，△ABC和△DBE为等腰直角三角形，且AD=2，AE=2$\sqrt{3}$，求AC的长．
如图，在△ABC中，BC=10，cosC=$\frac{1}{8}$，AC=8，求∠B的正切值．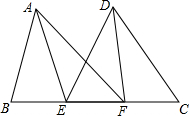
已知：点B，E，F，C在同一条直线上，AB=CD，BF=CE，AE=DF．求证：AF=DE．