题目内容
6.如图,△ABC中,∠BAC=90°AB=6,AC=8,在△ABC左边有一边长为4正方形从B点开始沿直线BC方向移动,直到不再与△ABC有重叠结束,若设平移的距离为t,正方形与△ABC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.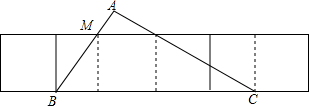
分析 自变量分6个区间讨论:①0<t≤3,②3<t≤4,③4<t≤$\frac{14}{3}$,④$\frac{14}{3}$<t≤7,⑤7<t≤10,⑥10<t≤14,根据三角形面积公式和梯形的面积公式即可求解.
解答 解:①0<t≤3,S=$\frac{1}{2}$t×$\frac{4}{3}$t=$\frac{2}{3}$t2;
②3<t≤4,S=$\frac{1}{2}$(t-3+t)×4=4t-6;
③4<t≤$\frac{14}{3}$,S=4×4-$\frac{1}{2}$[4-(t-3)]×$\frac{4}{3}$[4-(t-3)]=-$\frac{2}{3}$t2+$\frac{4}{3}$t-$\frac{50}{3}$;
④$\frac{14}{3}$<t≤7,S=4×4-$\frac{1}{2}$(t-$\frac{14}{3}$)×$\frac{3}{4}$(t-$\frac{14}{3}$)=-$\frac{3}{8}$t2+$\frac{7}{2}$t-$\frac{47}{6}$;
⑤7<t≤10,S=$\frac{1}{2}$[$\frac{3}{4}$(10-t)+$\frac{3}{4}$(10-t+4)]×4=36-3t;
⑥10<t≤14,S=$\frac{1}{2}$[4-(t-10)]×$\frac{3}{4}$[4-(t-10)]=$\frac{3}{8}$(t-14)2.
点评 考查了动点问题的函数图象,函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.注意分类思想的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
11.已知锐角α的余弦值是0.6,则锐角α的正切值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
18.九(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
(1)甲队成绩的中位数是9.5分,乙队成绩的众数是10分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分,若想从两队中选一个成绩较为稳定的队参加比赛,那么你认为该选哪个队参赛?为什么?
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分,若想从两队中选一个成绩较为稳定的队参加比赛,那么你认为该选哪个队参赛?为什么?
15.下列计算正确的是( )
| A. | -22=-4 | B. | -1-3=-2 | C. | (-3)2=6 | D. | (-1)3=1 |