题目内容
5．如图，两条直线相交只有1个交点，三条直线相交最多有3个交点，四条直线相交最多有6个交点，五条直线相交最多有10个交点，六条直线相交最多有15个交点，n条直线相交最多有$\frac{n（n-1）}{2}$个交点．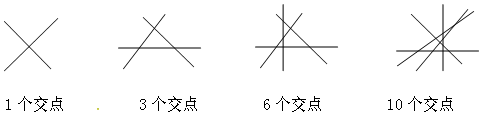
分析 根据图形相邻两个图形的交点个数的差为从2开始的连续整数，然后列式计算即可得解；
根据图形列出交点个数的算式，然后计算即可得解．
解答 解：三条直线交点最多为1+2=3个，
四条直线交点最多为3+3=6个，
五条直线交点最多为6+4=10个，
六条直线交点最多为10+5=15个；
n条直线交点最多为1+2+3+…+（n-1）=$\frac{n（n-1）}{2}$．
故答案为：15；$\frac{n（n-1）}{2}$．
点评 本题考查了直线、射线、线段，发现规律题，观察出相邻两个图形的交点个数的差为连续整数是解题的关键．
练习册系列答案
相关题目
15．已知（-1，y1），（1，y2）是直线y=-9x+6上的两个点，则y1，y2的大小关系是（ ）
| A． | y1＞0＞y2 | B． | y1＞y2＞0 | C． | y2＞0＞y1 | D． | 0＞y1＞y2 |
16．半径为1的圆的外切直角三角形的面积的最小值为（ ）
| A． | 3-$2\sqrt{2}$ | B． | 3+$2\sqrt{2}$ | C． | 6-4$\sqrt{2}$ | D． | 6+4$\sqrt{2}$ |
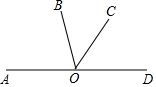如图，已知点O是直线AD上一点，且∠BOC=$\frac{1}{3}$∠AOC=$\frac{2}{3}$∠COD．求∠BOC的度数．
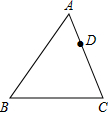如图，在△ABC中，AB=8，AC=6，点D在AC上，AD=2，若点E在AB上，以A，D，E为顶点的三角形与△ABC相似．求AE的长．
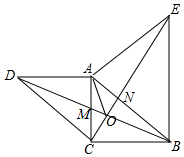已知：如图，△ABC中，∠ACB=90°，AC=BC，以A为直角顶点，分别以AC、AB为一直角边，在△ABC外做等腰直角△ACD和△ABE，连接BD、CE交与点O．
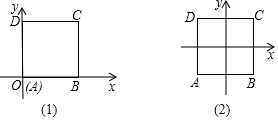已知正方形ABCD，边长为1cm．
如图所示，AO⊥FD，OD为∠BOC的平分线，OE为射线OB的反向延长线，若∠AOB=40°，求∠EOF、∠COE的度数．