题目内容
17.一个多边形的边数每增加1条时,它的内角和②,它的外角和③.(在下列5个备选答案中,把你认为正确答案的序号填在相应的空格内.①增加1;②增加180°;③不变;④增加360°;⑤不确定).分析 利用n边形的内角和公式(n-2)•180°(n≥3)且n为整数),多边形外角和为360°即可解决问题.
解答 解:根据n边形的内角和可以表示成(n-2)•180°,
可以得到每增加1条边时,边数变为n+1,
则内角和是(n-1)•180°,因而内角和增加:(n-1)•180°-(n-2)•180°=180°.
多边形外角和为360°,保持不变.
故答案为:②,③.
点评 本题主要考查了多边形的内角和公式和外角和定理,是需要熟练掌握的内容.

练习册系列答案
相关题目
7. 如图,由A到B有(1)、(2)、(3)三条路线,最短路线选(1)的理由是( )
如图,由A到B有(1)、(2)、(3)三条路线,最短路线选(1)的理由是( )
 如图,由A到B有(1)、(2)、(3)三条路线,最短路线选(1)的理由是( )
如图,由A到B有(1)、(2)、(3)三条路线,最短路线选(1)的理由是( )| A. | 两点确定一条直线 | B. | 两点确定一条射线 | ||
| C. | 两点之间距离最短 | D. | 两点之间线段最短 |
12.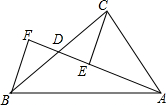 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
①△BDF≌△CDE;②CE=BF;③ABD和△ACD的面积相等;④BF∥CE.
 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )①△BDF≌△CDE;②CE=BF;③ABD和△ACD的面积相等;④BF∥CE.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.二元一次方程3x+2y=15在自然数范围内的解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,将一张矩形纸片ABCD沿着过点A的折痕翻折,使点B落在AD边上的点F,折痕交BC于点E,将折叠后的纸片再次沿着另一条过点A的折痕翻折,点E恰好与点D重合,此时折痕交DC于点G,则CG:GD的值为$\frac{\sqrt{2}}{2}$.
如图,将一张矩形纸片ABCD沿着过点A的折痕翻折,使点B落在AD边上的点F,折痕交BC于点E,将折叠后的纸片再次沿着另一条过点A的折痕翻折,点E恰好与点D重合,此时折痕交DC于点G,则CG:GD的值为$\frac{\sqrt{2}}{2}$. 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题: