Question

16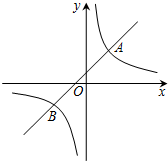．如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A（2，3），B（-3，n）两点．
（1）求一次函数和反比例函数的解析式；
（2）若P是y轴上一点，且满足△PAB的面积是5，直接写出点P的坐标．

Answer 1

分析 （1）可先把A代入反比例函数解析式，求得m的值，进而求得n的值，把A，B两点分别代入一次函数解析式即可．
（2）令x=0求出y的值，确定出C坐标，得到OC的长，三角形ABP面积由三角形ACP面积与三角形BCP面积之和求出，由已知的面积求出PC的长，即可求出OP的长．

解答 解：（1）∵点A（2，3）在y=$\frac{m}{x}$上，
∴m=6，
∴反比例函数解析式为y=$\frac{6}{x}$；
又∵点B（-3，n）在y=$\frac{6}{x}$上，
∴n=-2，
∴点B的坐标为（-3，-2），
把A（2，3）和B（-3，-2）两点的坐标代入一次函数y=kx+b得$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$，
∴一次函数的解析为y=x+1．
（2）对于一次函数y=x+1，令x=0求出y=1，即C（0，1），OC=1，
根据题意得：S_△ABP=$\frac{1}{2}$PC×2+$\frac{1}{2}$PC×3=5，
解得：PC=2，
所以，P（0，3）或（0，-1）．

点评 此题考查了一次函数与反比例函数的交点问题，涉及的知识有：待定系数法求函数解析式，坐标与图形性质，以及三角形的面积求法，熟练掌握待定系数法是解本题的关键．