题目内容
2.(1)已am=2,an=3,求am+n的值; a3m-2n的值.(2)已3×9m×27m=321,(-m2)3÷(m3•m2)的值.
分析 (1)根据同底数幂的乘法底数不变指数相加,可得答案;根据幂的乘方,可得同底数幂的除法,根据同底数幂的除法,可得答案;
(2)根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得底数相等的幂,可得关于m的方程,根据解方程,可得m的值,根据积的乘方、同底数幂的乘法,可得同底数幂的除法,再根据同底数幂的除法,可得答案.
解答 解:(1)am+n=am×an=2×3=6;
a3m=(am)3=23=8,a2n=(an)2=32=9,
a3m-2n=a3m÷a2n=8÷9=$\frac{8}{9}$;
(2)3×9m×27m=3×32m×33m=31+2m+3m=321,
1+2m+3m=21.解得m=4.
(-m2)3÷(m3•m2)=-m6÷m5=-m,
当m=4时,-m=-4.
点评 本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键,注意(-m2)3=-m6.

练习册系列答案
相关题目
10.在平面直角坐标系中,点A(-1,5),将点A向右平移2个单位、再向下平移3个单位得到点A1;再将线段OA1绕原点O顺时针旋转90°得到OA2.则A2的坐标为( )
| A. | (-1,2) | B. | (2,1) | C. | (2,-1) | D. | (3,-1) |
7.点P(5,-4)关于y轴对称点是( )
| A. | (5,4) | B. | (5,-4) | C. | (4,-5) | D. | (-5,-4) |
12.若关于x,y的方程组$\left\{\begin{array}{l}{5x+3ay=16}\\{-bx+4y=15}\end{array}\right.$(其中a,b是常数)的解为$\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$,则方程组 $\left\{\begin{array}{l}{5(x+1)+3a(x-2y)=16}\\{-b(x+1)+4(x-2y)=15}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5.5}\\{y=-1}\end{array}\right.$ |
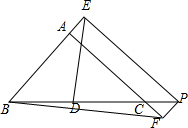 如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.
如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.