题目内容
4.在下列各数中0,$\frac{25}{4}$,a2+1,-(-$\frac{1}{3}$)2,-(-5)2,x2+2x+2,|a-1|,|a|-1,$\sqrt{16}$,有平方根的个数是6个.分析 先化简各数,然后判断它们的正负情况,最后依据平方根的性质回答即可.
解答 解:0的平方根是0;
$\frac{25}{4}$是一个正数,有平方根;
a2+1≥1,是一个正数,有平方根;
-(-$\frac{1}{3}$)2<0,没有平方根;
-(-5)2<0,没有平方根;
x2+2x+2≥1,有平方根;
|a-1|≥0,有平方根;
当a=0时,|a|-1<0,没有平方根,
$\sqrt{16}$=4,是一个正数,有平方根.
其中有平方根的有6个.
故答案为:6.
点评 本题主要考查的是平方根的性质,掌握平方根的性质是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
9.点M(-1,2)关于x轴对称的点的坐标为( )
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (2,-1) |

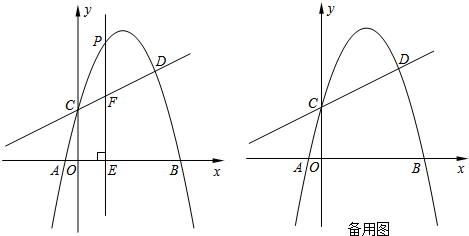
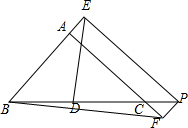 如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.
如图,点P是等腰Rt△ABC的底边BC延长线上的一点,过P作BA、AC的垂线,垂足分别为E、F.