题目内容
在直角坐标系中，将点P(－3,2)向沿y轴方向向上平移4个单位长度后，得到的点坐标为( )
A. (－3,6) B. (1,2) C. (－7,2) D. (－3，－2)
A
【解析】因为点沿y轴向上移动,横坐标不变,纵坐标加上平移单位,将点P(－3,2)向沿y轴方向向上平移4个单位长度后,得到的点坐标为(－3,6),故选A.
判断对错：对顶角是中心对称图形；________________
对
【解析】根据对顶角的定义及中心对称图形的定义，易得对顶角是中心对称图形.
故答案：对. 不论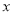
, 
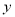为任何实数， 
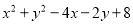的值总是（ ）
A. 正数 B. 负数 C. 非负数 D. 非正数
A
【解析】x²+y²－4x-2y+8=(x²－4x+4)+(y²-2y+1)+3=(x-2)2+(y-1)2+3≥3，
不论x,y为任何实数,x²+y²－4x-2y+8的值总是大于等于3，
故选A. 如图，直线l1在平面直角坐标系中，直线l1与y轴交于点A，点B(－3,3)也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l1上．
(1)求点C的坐标和直线l1的解析式；
(2)若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l1上；
(3)已知直线l2：y＝x＋b经过点B，与y轴交于点E，求△ABE的面积．
(1) C的坐标为(－2,1)，直线l1的解析式为y＝－2x－3；(2)点D在直线l1上；(3)△ABE的面积为13.5.
【解析】试题分析：（1）∵B（﹣3，3），将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，
∴﹣3+1=﹣2，3﹣2=1，∴C的坐标为（﹣2，1），设直线l1的解析式为y=kx+c，∵点B、C在直线l1上，∴代入得：，解得：k=﹣2，c=﹣3，∴直线... 在平面直角坐标中，△ABC的三个顶点的坐标分别是A(－2,3)，B(－4，－1)，C(2,0)，将△ABC沿x轴方向向左平移_______至△A1B1C1的位置，点A、B、C的对应点分别是A1、B1、C1，使点C1在原点处．
2个单位
【解析】因为C(2,0)沿x轴方向向左平移后对应对应点C1在原点处,即点C沿x轴方向向左平移2个单位,故答案为:2. （1）请在坐标系中画出二次函数y=x2﹣2x的大致图象；
（2）根据方程的根与函数图象的关系，将方程x2﹣2x=1的根在图上近似的表示出来（描点）；
（3）观察图象，直接写出方程x2﹣2x=1的根．（精确到0.1）
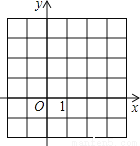
【解析】
（1）如下图，
y=x2﹣2x=（x﹣1） 2﹣1，
作出顶点，作出与x轴的交点，图象光滑．
（2）正确作出点M，N；
（3）写出方程的根为﹣0.4，2.4．
【解析】
（1）确定顶点坐标和与x轴y轴交点，作出图形；
（2）方程x2﹣2x=1的根就是二次函数y=x2﹣2x的函数值为1时的横坐标x的值；
（3）观察图象可知图象交点的横坐标即... 下列哪一个函数，其图象与x轴有两个交点（ ）
A. y=(x-23)2+155 B. y=(x+23)2+155
C. y= -(x-23)2-155 D. y= -(x+23)2+155
D
【解析】A、令y=0得，(x-23)2+155=0，移项得，(x-23)2= -155，方程无实根；
B、令y=0得，(x+23)2+155=0，移项得，(x+23)2= -155，方程无实根；
C、令y=0得，-(x-23)2-155=0，移项得，(x-23)2= -155，方程无实根；
D、令y=0得，-(x+23)2+155=0，移项得，(x+23)2=155，方... 若x2+2（m﹣1）x+36是完全平方式，则m=__．
7或﹣5
【解析】∵x2+2（m﹣1）x+36是完全平方式，
∴2（m﹣1）x=±2×6x,
∴m﹣1=±6,
∴m=7或m=-5. 已知△ABC中，AB＝AC，求证∠B＜90°，下面写出了用反证法证明过程中的四个步骤：①所以∠B＋∠C＋∠A＞180°，这与三角形内角和定理相矛盾；②所以∠B＜90°；③假设∠B≥90°；④那么由AB＝AC，得∠B＝∠C≥90°，即∠B＋∠C≥180°.这四个步骤正确的顺序应是_________(填序号)．
③④①②
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，然后根据已知条件得出与定理相矛盾，最后得出假设不成立，得出答案，故正确的序号是：③④①②．