题目内容
3.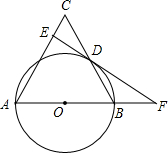 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,作DE⊥AC,垂足为点E,ED与AB的延长线交于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,作DE⊥AC,垂足为点E,ED与AB的延长线交于点F.(1)求证:ED为⊙O的切线.
(2)当BF=$\frac{1}{2}$AB,且CE=$\sqrt{3}$时,求AF的长.
分析 (1)连接OD,根据等腰三角形的性质得到∠ABC=∠C,∠ODB=∠OBD,等量代换得到∠C=∠ODB,根据平行线的判定定理得到OD∥AC,证得DE⊥OD,根据切线的判定即可得到结论;
(2)连接AD,根据圆周角定理得到AD⊥BC,根据已知条件得到BF=OB=OD=$\frac{1}{2}$OF,解直角三角形得到∠F=30°,求得∠DOF=60°,证得OD∥AE,根据平行线的性质得到∠CAB=∠DOB=60°,推出△ABC是等边三角形,由等边三角形的性质得到AB=BC,∠C=60°,求得CD=2CE=2$\sqrt{3}$,即可得到结论.
解答 (1)证明:连接OD,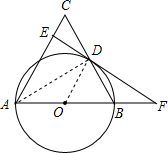 ∵AB=AC,
∵AB=AC,
∴∠ABC=∠C,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠C=∠ODB,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴ED为⊙O的切线.
(2)解:连接AD,
∵AB为⊙O的直径,
∴AD⊥BC,BC=2CD,
∵BF=$\frac{1}{2}$AB,
∴BF=OB=OD=$\frac{1}{2}$OF,
∴∠F=30°,
∵∠DOF=60°,
∵OD⊥EF,AE⊥EF,
∴OD∥AE,
∴∠CAB=∠DOB=60°,
∴△ABC是等边三角形,
∴AB=BC,∠C=60°,
∵CE=$\sqrt{3}$,
∴CD=2CE=2$\sqrt{3}$,
∴AB=BC=4$\sqrt{3}$,
∴BF=$\frac{1}{2}$AB=2$\sqrt{3}$,
∴AF=AB+BF=6$\sqrt{3}$.
点评 此题考查了切线的性质,圆周角定理,等腰三角形的性质,等边三角形的判定和性质,平行线的判定和性质,注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
18. 如图,直线AB、CD相交于点E,DF∥AB,若∠D=50°,则∠AEC的度数等于( )
如图,直线AB、CD相交于点E,DF∥AB,若∠D=50°,则∠AEC的度数等于( )
 如图,直线AB、CD相交于点E,DF∥AB,若∠D=50°,则∠AEC的度数等于( )
如图,直线AB、CD相交于点E,DF∥AB,若∠D=50°,则∠AEC的度数等于( )| A. | 130° | B. | 120° | C. | 150° | D. | 50° |
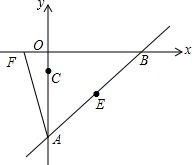 如图,已知点A(0,a),B(b,0),C(0,c),且|a+4|+$\sqrt{{b^2}-8b+16}$=0,(c+1)2≤0,点D与点C关于直线AB对称,
如图,已知点A(0,a),B(b,0),C(0,c),且|a+4|+$\sqrt{{b^2}-8b+16}$=0,(c+1)2≤0,点D与点C关于直线AB对称,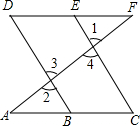 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证: 如图,将一个长方形纸条折成如图的形状,若已知∠2=55°,则∠1=110°.
如图,将一个长方形纸条折成如图的形状,若已知∠2=55°,则∠1=110°.