题目内容
13.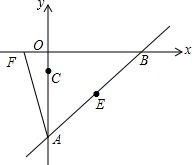 如图,已知点A(0,a),B(b,0),C(0,c),且|a+4|+$\sqrt{{b^2}-8b+16}$=0,(c+1)2≤0,点D与点C关于直线AB对称,
如图,已知点A(0,a),B(b,0),C(0,c),且|a+4|+$\sqrt{{b^2}-8b+16}$=0,(c+1)2≤0,点D与点C关于直线AB对称,(1)求直线AB的解析式和点C、D的坐标;
(2)点E在直线AB上,直接写出|EO-ED|的最大值和最小值及对应的点E的坐标;
(3)点F(-1,0),在平面内有一点P,使得△OAP∽△DAF,求点P的坐标.
分析 (1)由非负数的性质可求得a、b、c的值,从而得到点A、B、C的坐标,然后依据待定系数法可求得AB的解析式,由等腰直角三角形的性质和翻折的性质可证明△ADC为等腰直角三角形,从而可求得点D的坐标;
(2)由轴对称图形的性质可知EC=ED,由三角形的三边关系可知当点E与点A重合时,|EO-ED|有最大值,当EO=EC时,|EO-ED|有最小值;
(3)依据两边对应成立且夹角相等的两个三角形相似可知∠PAO=∠FAD且$\frac{AD}{OA}=\frac{FA}{PA}$,从而可求得点P的坐标,作P关于y轴对称点P′,由轴对称的性质可知△OAP′∽△DAF.
解答 解:(1)∵|a+4|+$\sqrt{{b^2}-8b+16}$=0,
∴a+4=0,b-4=0.
解得:a=-4,b=4.
∴A(0,-4)、B(4,0).
设直线AB的解析式为y=kx+b.
∵将A(0,-4)、B(4,0)代入得$\left\{\begin{array}{l}{b=-4}\\{4k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$,
∴直线AB的解析式为y=x-4.
∵(c+1)2≤0,(c+1)2≥0,
∴c+1=0.
解得:c=-1.
∴点C(0,-1).
如图1所示:
∵A(0,-4)、B(4,0),
∴OB=OA.
∴∠OAB=45°.
∵点C与点D关于AB对称,
∴∠DAE=45°,CA=DA=3.
∴∠CAD=90°.
∴点D的纵坐标为(3,-4).
(2)如图2所示:
∵点D与点C关于AB对称,
∴CE=DE.
∴|EO-ED|=|EO-ED|=|EO-EC|.
∴当点O、C、E在一条直线上时,|EO-EC|有最大值.
∴当点E的坐标为(0,-4)时,|EO-EC|的最大值为1,即|EO-ED|的最大值为1.
∵EO=EC时,|EO-ED|=|EO-EC|=0,
∴点E在OC的垂直平分线上.
∴点E的纵坐标为-$\frac{1}{2}$.
∵将y=-$\frac{1}{2}$代入y=x-4得:x=$\frac{7}{2}$,
∴E($\frac{7}{2}$,-$\frac{1}{2}$).
∴点E的坐标为($\frac{7}{2}$,-$\frac{1}{2}$)时,|EO-ED|的最小值为0.
(3)如图3所示:过点P作PG⊥AD,垂足为G.
当∠PAO=∠FAD且$\frac{AD}{OA}=\frac{FA}{PA}$时,△OAP∽△DAF.
∵∠PAO=∠FAD,
∴∠FAO=∠PAG.
∴$\frac{PG}{AG}=\frac{OF}{OA}$=$\frac{1}{4}$.
设PG=a,则AG=4a.则由勾股定理可知:AP=$\sqrt{P{G}^{2}+A{G}^{2}}$=$\sqrt{17}$a.
∵OF=1,OA=4,
∴AF=$\sqrt{17}$.
∴$\frac{3}{4}=\frac{\sqrt{17}}{\sqrt{17}a}$.
解得:a=$\frac{4}{3}$.
∴PG=$\frac{4}{3}$,AG=$\frac{16}{3}$.
∴点G的坐标为(-$\frac{16}{3}$,$-\frac{16}{3}$).
作点P关于y轴对称点P′,由轴对称图形的性质可知△OAP≌△OAP′,P′($\frac{16}{3}$,$-\frac{16}{3}$).
∵△OAP∽△DAF,
∴△OAP′∽△DAF.
综上所述,点P的坐标为(-$\frac{16}{3}$,$-\frac{16}{3}$)或($\frac{16}{3}$,$-\frac{16}{3}$)时,△OAP∽△DAF.
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式、非负数的性质、轴对称图形的性质、三角形的三边关系、相似三角形的判定,用含a的式子表示AP的长是解题的关键.

| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{8}×\sqrt{2}=4$ | C. | $2+\sqrt{3}=2\sqrt{3}$ | D. | $\frac{{\sqrt{10}}}{2}=\sqrt{5}$ |
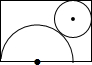 如图,在一张矩形硬纸板中剪下一个半圆形和一个圆形,使之恰好围成一个圆锥,则这个圆锥的侧面积S侧和底面积S底的关系是( )
如图,在一张矩形硬纸板中剪下一个半圆形和一个圆形,使之恰好围成一个圆锥,则这个圆锥的侧面积S侧和底面积S底的关系是( )| A. | S侧=S底 | B. | S侧=2S底 | C. | S侧=3S底 | D. | S侧=4S底 |
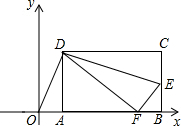 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为(16,3)或(4$\sqrt{5}$+6,2$\sqrt{5}$-2)或($\frac{43}{3}$,$\frac{7}{4}$).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为(16,3)或(4$\sqrt{5}$+6,2$\sqrt{5}$-2)或($\frac{43}{3}$,$\frac{7}{4}$).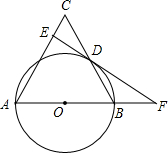 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,作DE⊥AC,垂足为点E,ED与AB的延长线交于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,作DE⊥AC,垂足为点E,ED与AB的延长线交于点F.