题目内容
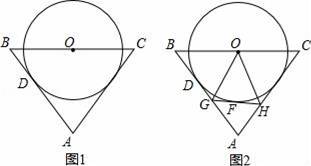
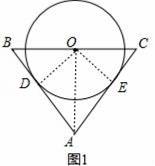
如图1,△ABC中,AB=AC,点O是BC的中点,以O为圆心的⊙O与AB边相切于点D.
(1)判断AC边与⊙O的位置关系,说明理由;
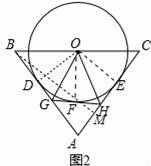
(2)如图2,若AB=5,BC=6,点F为⊙O上一动点,过点F作⊙O的切线分别交AD边、AC边于点G、H,连结OG、OH.
①设∠BAC=α,则∠GOH= (用含α的代数式表示);
②若△OGH是以GH为腰的等腰三角形,求BG的长.

【考点】圆的综合题.
【专题】综合题.
【分析】(1)作OE⊥AC于E,连结OA、OD,如图1,先利用切线的性质得OD⊥AB,再根据等腰三角形的性质,由AB=AC,点O是BC的中点得到AO平分∠BAC,则利用角平分线的性质得到OE=OD,于是可根据切线的判定方法得到AC为⊙O的切线;
(2)①作OE⊥AC于E,BM⊥AC于M,连结OF、OD,如图2,由切线的性质得OF⊥GH,由切线长定理得GD=GF,HF=HE,于是可根据角平分线定理的逆定理得∠DOG=∠FOG,∠EOH=∠FOH,则∠GOH=
 ∠DOE,再由四边形内角和得到∠DOE+∠A=180°,所以∠GOEH=90°﹣
∠DOE,再由四边形内角和得到∠DOE+∠A=180°,所以∠GOEH=90°﹣
 α;
α;
②在图1中,AB=5,OB=OC=
 BC=3,利用勾股定理和面积法先计算出OA=5,OD=
BC=3,利用勾股定理和面积法先计算出OA=5,OD=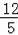
 ,BD=
,BD=
 ,BM=
,BM=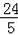
 ,AM=
,AM=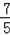
 ,接着分类讨论:当GH=GO时,∠GHO=∠GOH=90°﹣
,接着分类讨论:当GH=GO时,∠GHO=∠GOH=90°﹣
 α,则∠OGH=α,于是可判断Rt△OGF∽Rt△BAM,利用相似比可计算出GF=
α,则∠OGH=α,于是可判断Rt△OGF∽Rt△BAM,利用相似比可计算出GF=
 ,则DG=GF=
,则DG=GF=
 ,所以BG=BD+DG=
,所以BG=BD+DG=
 ;当GH=OH时,同样可证明Rt△OHF∽Rt△BAM,利用相似比可计算出FH=
;当GH=OH时,同样可证明Rt△OHF∽Rt△BAM,利用相似比可计算出FH=
 ,OH=
,OH=
 ,则GH=OH=
,则GH=OH=
 ,所以GF=GH﹣FH=
,所以GF=GH﹣FH=
 =DG,则BG=BD+DG=
=DG,则BG=BD+DG=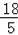
 .
.
【解答】解:(1)AC边与⊙O相切.理由如下:
作OE⊥AC于E,连结OA、OD,如图1,
∵以O为圆心的⊙O与AB边相切于点D,
∴OD⊥AB,
∵AB=AC,点O是BC的中点,
∴AO平分∠BAC,
∴OE=OD,
∴AC为⊙O的切线;
(2)①作OE⊥AC于E,BM⊥AC于M,连结OF、OD,如图2,
∵GH为⊙O的切线,
∴OF⊥GH,
∵AB和AC为⊙O的切线,
∴GD=GF,HF=HE,
∴∠DOG=∠FOG,∠EOH=∠FOH,
∴∠GOH=
 ∠DOE,
∠DOE,
∵∠DOE+∠A=180°,
∴∠GOEH=
 (180°﹣α)=90°﹣
(180°﹣α)=90°﹣
 α,
α,
故答案为90°﹣
 α;
α;
②在图1中,AB=5,OB=OC=
 BC=3,则OA=
BC=3,则OA=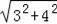
 =5,
=5,
∵
 OD•AB=
OD•AB=
 OB•OA,
OB•OA,
∴OD=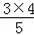
 =
=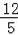
 ,
,
在Rt△BOD中,BD=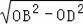
 =
=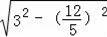
 =
=
 ,
,
在图2中,
∵
 BM•AC=
BM•AC=
 BC•OA,
BC•OA,
∴BM=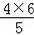
 =
=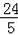
 ,
,
在Rt△ABM中,AM=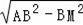
 =
=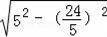
 =
=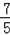
 ,
,
当GH=GO时,∠GHO=∠GOH=90°﹣
 α,
α,
∴∠OGH=180°﹣2(90°﹣
 α)=α,
α)=α,
∴Rt△OGF∽Rt△BAM,
∴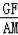
 =
=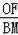
 ,即
,即
 =
=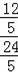
 ,解得GF=
,解得GF=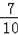
 ,
,
∴DG=GF=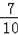
 ,
,
∴BG=BD+DG=
 +
+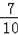
 =
=
 ;
;
当GH=OH时,∠GHO=∠GOH=90°﹣
 α,则∠OHG=α,
α,则∠OHG=α,
∴Rt△OHF∽Rt△BAM,
∴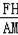
 =
=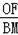
 =
=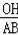
 ,即
,即
 =
=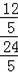
 =
=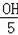
 ,解得FH=
,解得FH=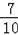
 ,OH=
,OH=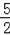

∴GH=OH=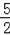
 ,
,
∴GF=GH﹣FH=
 ﹣
﹣
 =
=
 ,
,
∴DG=GF=
 ,
,
∴BG=BD+DG=
 +
+
 =
=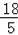
 ,
,
综上所述,BG的长为
 或
或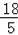
 .
.


【点评】本题考查了圆的综合题:熟练掌握圆的切线的判定与性质、切线长定理和等腰三角形的性质;会利用相似比和勾股定理计算线段的长;会运用分类讨论的思想解决数学问题.

 ,使它的图像与正方形OABC的边有公共点,这个函数的解析式可以是 .
,使它的图像与正方形OABC的边有公共点,这个函数的解析式可以是 .
 、
、 被直线
被直线 所截,那么
所截,那么 的同位角是( )
的同位角是( ) B.
B. C.
C. D.
D.






 与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).

 ,求代数式(x+1)2-2x+y(y-2x)的值.
,求代数式(x+1)2-2x+y(y-2x)的值.