题目内容
14. 如图,在平面直角坐标系中,点O为坐标原点,点A、B的坐标分别为(0,a)、(-a,0)(a>0),点C是点B关于y轴的对称点,连接AB、AC,△ABC的面积为18.
如图,在平面直角坐标系中,点O为坐标原点,点A、B的坐标分别为(0,a)、(-a,0)(a>0),点C是点B关于y轴的对称点,连接AB、AC,△ABC的面积为18.①点C的坐标是(3$\sqrt{2}$,0);
②动点D从动点B出发,沿x轴正方向运动,动点E从点A出发,沿y轴正方向运动,两点同时出发,运动速度均为1个单位长度/秒,连接DE,在DE右侧,以DE为斜边作等腰直角△DEF,设动点D的运动时间为t秒,请用含t的代数式表示点F的坐标;
③在②的条件下,连接AD、OF,作线段AD的垂直平分线,与直线OF相交于点G,连接DG,直线DG与y轴相交于点K,当CA=CD时,求点K的坐标?
分析 ①根据三角形面积公式,列出方程即可解决问题.
②如图1中,作FM⊥BC于M,FN⊥OA于N,由△FNE≌△FMD,得到FN=FM,EN=DM,四边形FMON是正方形,设正方形边长为m,根据EN=DM,列出方程即可解决问题.
③分两种情形,如图2中,当点D在线段BC上时,如图3中,当点D在BC的延长线上时,分别求出直线DG解析式即可解决问题.
解答 解:①∵点C是点B关于y轴的对称点,B(-a,0),
∴点C坐标(a,0),
∵$\frac{1}{2}$•2a•a=18,a>0,
∴a=3$\sqrt{2}$,
∴点C坐标(3$\sqrt{2}$,0).
故答案为(3$\sqrt{2}$,0)
②如图1中,作FM⊥BC于M,FN⊥OA于N.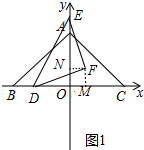
∵∠EFD=∠NFM=90°,
∴∠NFE=∠DFM,
在△FNE和△FMD中,
$\left\{\begin{array}{l}{∠NFE=∠DFM}\\{∠FNE=∠FMD}\\{EF=DF}\end{array}\right.$,
∴△FNE≌△FMD,
∴FN=FM,EN=DM,四边形FMON是正方形,设正方形边长为m,
则3$\sqrt{2}$+m-t=3$\sqrt{2}$+t-m,
∴m=t,
∴点F坐标为(t,t).
③如图2中,当点D在线段BC上时,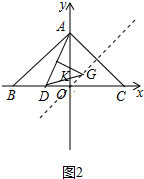
由②可知直线OF解析式为y=x,
∵CA=CD=6,
∴点D坐标(3$\sqrt{2}$-6,0),
设直线AD解析式为y=kx+b,则$\left\{\begin{array}{l}{b=3\sqrt{2}}\\{(3\sqrt{2}-6)k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\sqrt{2}+1}\\{b=3\sqrt{2}}\end{array}\right.$,
∴直线AD的解析式为y=($\sqrt{2}$+1)x+3$\sqrt{2}$,
线段AD中垂线的解析式为y=(1-$\sqrt{2}$)x+6-3$\sqrt{2}$,
由$\left\{\begin{array}{l}{y=x}\\{y=(1-\sqrt{2})x+6-3\sqrt{2}}\end{array}\right.$解得,$\left\{\begin{array}{l}{x=3\sqrt{2}-3}\\{y=3\sqrt{2}-3}\end{array}\right.$,
∴点G坐标(3$\sqrt{2}$-3,3$\sqrt{2}$-3).
设直线DG为y=mx+n,则$\left\{\begin{array}{l}{(3\sqrt{2}-3)m+n=3\sqrt{2}-3}\\{(3\sqrt{2}-6)m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\sqrt{2}-1}\\{n=9\sqrt{2}-9}\end{array}\right.$,
∴直线DG解析式为y=($\sqrt{2}$-1)x+9$\sqrt{2}$-9,
∴点K坐标为(0,9$\sqrt{2}$-9).
如图3中,当点D在BC的延长线上时,
由题意可得直线AD解析式为y=(1-$\sqrt{2}$)x+3$\sqrt{2}$,
线段AD的垂直平分线为y=($\sqrt{2}$+1)x-3$\sqrt{2}$-6,
由$\left\{\begin{array}{l}{y=x}\\{y=(\sqrt{2}+1)x-3\sqrt{2}-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3+3\sqrt{2}}\\{y=3+3\sqrt{2}}\end{array}\right.$,
∴点G坐标(3+3$\sqrt{2}$,3+3$\sqrt{2}$),
∴可得直线DG解析式为y=(-1-$\sqrt{2}$)x+12+9$\sqrt{2}$,
∴点K坐标为(0,12+9$\sqrt{2}$).
点评 本题考查几何变换综合题、全等三角形的判定和性质、一次函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会利用方程组求两个函数的交点坐标,属于中考压轴题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | $\frac{5}{sin20°}$ | B. | $\frac{5}{cos20°}$ | C. | $\frac{5}{tan20°}$ | D. | 5tan20° |
 如图所示为黄冈市十二月份某一天的天气预报,这天最高气温比最低气温高( )
如图所示为黄冈市十二月份某一天的天气预报,这天最高气温比最低气温高( )| A. | -30℃ | B. | 7℃ | C. | 3℃ | D. | -7℃ |
| A. | ac>bc | B. | ac<bc | C. | ac2>bc2 | D. | ac2≥b c2 |
| A. | 先右转30°,后左转30° | B. | 先右转30°,后右转60° | ||
| C. | 先右转30°,后左转60° | D. | 先右转30°,后左转150° |
 根据如图的程序,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…,第2015次输出的结果为( )
根据如图的程序,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…,第2015次输出的结果为( ) 如图,大正方形的面积为1,很明显,中间的竖线将正方形一分为二,所以左边的长方形的面积为$\frac{1}{2}$,同样右边长方形中间的横线将该长方形又一分为二,所以右下角正方形的面积为$\frac{1}{4}(\frac{1}{{2}^{2}})$,…由此图,可以推算出$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{10}}$的结果为$\frac{1023}{1024}$.
如图,大正方形的面积为1,很明显,中间的竖线将正方形一分为二,所以左边的长方形的面积为$\frac{1}{2}$,同样右边长方形中间的横线将该长方形又一分为二,所以右下角正方形的面积为$\frac{1}{4}(\frac{1}{{2}^{2}})$,…由此图,可以推算出$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{10}}$的结果为$\frac{1023}{1024}$.