题目内容
3.如图,在Rt△AOB中,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.(Ⅰ)如图①当E点恰好落在线段AB上时,求E点坐标;
(Ⅱ)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,当E点到达△AOB的外面,且点D在点B左侧时,写出y与x的函数关系式,并写出自变量x的取值范围;
(Ⅲ)在(Ⅰ)问的条件下,将△ODE在线段OB上向右平移如图②,图中是否存在一条与线段OO′始终相等的线段?如果存在,请直接指出这条线段;如果不存在,请说明理由.

分析 (1)由题意作辅助线,作EH⊥OB于点H,由BO=4,求得OE,然后求出OH,EH,从而得出点E的坐标;
(2)根据题意,当E点到达△AOB的外面,且点D在点B左侧时,2<x<4即可;
(3)假设存在,由OO′=4-2-DB,而DF=DB,从而得到OO′=EF;
解答 解:(1)作EH⊥OB于点H,
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=$\frac{1}{2}$OB=2.
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=$\sqrt{3}$,
∴E(1,$\sqrt{3}$).
(2)当2<x<4,符合题意,
如图,
所求重叠部分四边形OD′NE的面积为:
S△OD′E-S△E′EN=$\frac{\sqrt{3}}{4}$x2-$\frac{1}{2}$E′E×EN
=$\frac{\sqrt{3}}{4}$x2-$\frac{x-2}{2}$×$\sqrt{3}$(x-2)
=-$\frac{\sqrt{3}}{4}$x2+2$\sqrt{3}$x-2$\sqrt{3}$
(3)存在线段EF=OO'.
∵∠ABO=30°,∠EDO=60°
∴∠ABO=∠DFB=30°,
∴DF=DB.
∴OO′=4-2-DB=2-DB=2-DF=ED-FD=EF
点评 此题是几何变换综合题,主要考查利用三角函数求线段长度,动点问题是中考的重点内容,此题难度较大.

练习册系列答案
相关题目
12.已知关于x的一元二次方程x2-2x-k=0有两个不相等的实数根,则实数k的取值范围是( )
| A. | k≥1 | B. | k>1 | C. | k≥-1 | D. | k>-1 |
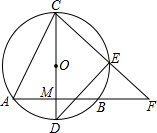 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交AB的延长线于点F,连结DE.
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交AB的延长线于点F,连结DE.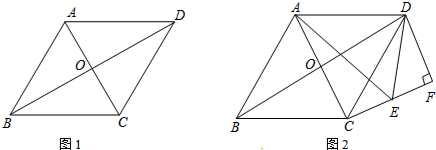
 如图,一次函数y=$\frac{1}{2}$x+2的图象在x、y轴上的交点为A、B,点P是该一次函数的图象上位于x轴上方的一点,作PQ⊥x轴于点Q,以PQ的右侧作正方形PQMN.
如图,一次函数y=$\frac{1}{2}$x+2的图象在x、y轴上的交点为A、B,点P是该一次函数的图象上位于x轴上方的一点,作PQ⊥x轴于点Q,以PQ的右侧作正方形PQMN.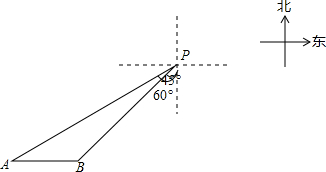 一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?