题目内容
12．已知关于x的一元二次方程x2-2x-k=0有两个不相等的实数根，则实数k的取值范围是（ ）| A． | k≥1 | B． | k＞1 | C． | k≥-1 | D． | k＞-1 |
分析 根据判别式的意义得到△=（-2）2+4k＞0，然后解不等式即可．
解答 解：∵关于x的一元二次方程x2-2x-k=0有两个不相等的实数根，
∴△=（-2）2+4k＞0，
解得k＞-1．
故选：D．
点评 此题考查了一元二次方程根的分布，一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
应用题作业本系列答案
相关题目
如图，AB为东西走向的一条公路，C是公路旁边的一个村子，现在准备从村庄C修一条公路CD到公路AB，在A点时测得村庄C在它的北偏东45°方向上，沿正东方向4千米后到达B处，此时村庄C在它的北偏西55°方向上，求公路CD的最短长度．（结果精确到0.1千米，参考数据：sin55°≈0.8192，cos55°≈0.5736，tan55°≈1.4281）
如图，在△ABC中，∠A=63°，直线MN∥BC，且分别与AB，AC相交于点D，E，若∠AEN=133°，则∠B的度数为70°．
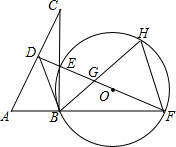如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD、FH．
二次函数y=ax2+bx+c的图象如图所示，那么一次函数y=ax+b的图象大致是（ ）
1．
如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（ ）
如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（ ）| A． | $\sqrt{10}$ | B． | 2$\sqrt{2}$ | C． | 3 | D． | 2$\sqrt{5}$ |