题目内容
13.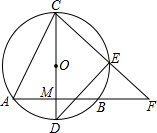 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交AB的延长线于点F,连结DE.
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交AB的延长线于点F,连结DE.(1)求证:△CDE∽△CFM;
(2)求⊙O的半径;
(3)求CE•CF的值.
分析 (1)直径所对的圆周角是直角,再用公共角直接得到△CDE∽△CFM;
(2)连结OB,设OM=3k,则MD=2k,OD=5k,根据垂径定理由直径CD⊥AB得到BM=AM=$\frac{1}{2}$AB=4,在Rt△OBM中,OB=5k,OM=3k,根据勾股定理得BM=4k,
则4k=4,解得k=1,于是得到圆O的半径为5;
(3)连结AE,如图,在Rt△ACM中,CM=OC+OM=8,AM=4,由勾股定理计算出AC2=AM2+CM2=80,根据垂径定理由直径CD⊥AB得到弧AC=弧BC,在根据圆周角定理得∠AEC=∠CAF,易证得△CAE∽△CFA,得到相似比,然后根据比例性质得CE•CF=AC2=80.
解答 证明:(1)∵直径CD⊥AB于M,
∴∠CMF=∠CED=90°,
∵∠DCE=∠FCM,
∴△CDE∽△CFM,
(2)连结OB,设OM=3k,则MD=2k,OD=5k
∵直径CD⊥AB,
∴BM=AM=$\frac{1}{2}$AB=4,
在Rt△OBM中,OB=5k,OM=3k,
∴BM=4k,
∴4k=4,
∴k=1,
∴⊙O的半径为5;
(3)连结AE,在Rt△ACM中,CM=OC+OM=5+3=8,AM=4,
∴AC2=AM2+CM2=16+64=80,
∵直径CD⊥AB,
∴$\widehat{AC}=\widehat{BC}$,
∴∠AEC=∠CAF,
又∵∠ACF=∠FCA,
∴△CAE∽△CFA,
∴$\frac{AC}{CF}=\frac{CE}{AC}$,
∴CE•CF=AC2=80.
点评 此题是圆的综合题,主要考查了圆中证明三角形相似的方法,相似三角形的性质和判定,勾股定理,解本题的关键是勾股定理的灵活运用.

练习册系列答案
相关题目
3.某班组织了一次读书活动,统计了10名同学在一周内累计的读书时间,如表所示,对于这10个同学的一周累计读书时间,下列说法错误的是( )
| 一周内累计的读书时间(小时) | 6 | 8 | 10 | 11 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 众数是8 | B. | 中位数是9 | C. | 平均数是9 | D. | 方差是1.5 |
1.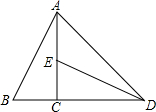 如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
 如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
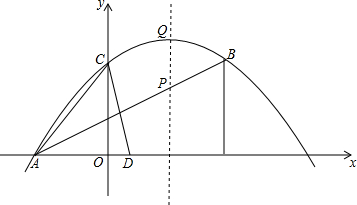 如图,抛物线y=ax2+bx+4的图象经过A(-3,0),B(5,4),与y轴交于点C.
如图,抛物线y=ax2+bx+4的图象经过A(-3,0),B(5,4),与y轴交于点C.
 如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)
如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)