题目内容
19．要使得式子$\sqrt{x-4}+\root{3}{\frac{1}{x-6}}$有意义，则x取值范围为x≥4且x≠6．分析 根据分式及二次根式有意义的条件求解x的取值范围．
解答 解：由题意得，$\left\{\begin{array}{l}{x-4≥0}\\{x-6≠0}\end{array}\right.$，
解得：x≥4且x≠6．
故答案为：x≥4且x≠6．
点评 本题考查了二次根式及分式有意义的条件，解答本题的关键是掌握二次根式有意义被开方数为非负数，分式有意义分母不为零．
练习册系列答案
相关题目
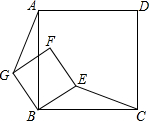如图，正方形ABCD和正方形GBEF，连接AG、CE，猜想CE与AG的位置关系，并证明你的猜想．
如图，点E为正方形ABCD的边CD的中点，点F在AD上，CF交AE于点G，且∠CGE=45°，AE=$\sqrt{5}$，则CF的长为$\frac{2}{3}$$\sqrt{10}$．
如图，在△ABC中，∠ACB=90°，CD⊥AB，求证：△ACD∽△ABC∽△CBD．