题目内容
8.已知△ABC∽△DEF,且AB:BC:CA=2:3:4,若△DEF的周长为27,则△DEF的各边长分别为6、9、12.分析 根据相似三角形的性质求出△DEF的三边之比,根据题意列出方程,解方程即可.
解答 解:∵△ABC∽△DEF,AB:BC:CA=2:3:4,
∴DE:EF:FD=2:3:4,
设DE、EF、FD的长分别为2x、3x、4x,
由题意得,2x+3x+4x=27,
解得x=3.
则DE、EF、FD的长分别为6、9、12.
故答案为:6、9、12.
点评 本题考查的是相似三角形的性质以及一元一次方程的应用,掌握相似三角形的对应角相等,对应边的比相等是解题的关键.

练习册系列答案
相关题目
17.关于x的方程x2+2kx+k-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
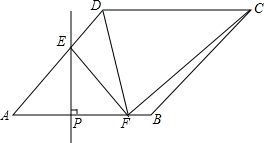 如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一个动点,过点P作PE⊥AB交直线AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=$\sqrt{2}$或2+$\sqrt{2}$..
如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一个动点,过点P作PE⊥AB交直线AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=$\sqrt{2}$或2+$\sqrt{2}$..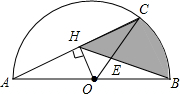 如图,AB为半圆的直径,弧AC为弧CB的两倍,OH⊥AC于点H,BH与OC交于E,己知AC=2$\sqrt{3}$.
如图,AB为半圆的直径,弧AC为弧CB的两倍,OH⊥AC于点H,BH与OC交于E,己知AC=2$\sqrt{3}$.