题目内容
观察下列各式:
-a,
a2,-
a3,
a4,-
a5,
a6,…
(1)写出第2014个和2015个单项式;
(2)写出第n个单项式.
-a,
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
(1)写出第2014个和2015个单项式;
(2)写出第n个单项式.
考点:单项式
专题:规律型
分析:(1)由单项式的排列规律即可求出第2014个和2015个单项式;
(2)由单项式的排列规律即可求出第n个单项式.
(2)由单项式的排列规律即可求出第n个单项式.
解答:解:(1)由-a,
a2,-
a3,
a4,-
a5,
a6,…
可得第n项的表达式为(-1)n
,
所以第2014个单项式为
,第2015个单项式为-
.
(2)由单项式的特点可得第n个单项式为(-1)n
.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
可得第n项的表达式为(-1)n
| an |
| 2n-1 |
所以第2014个单项式为
| a2014 |
| 22013 |
| a2015 |
| 22014 |
(2)由单项式的特点可得第n个单项式为(-1)n
| an |
| 2n-1 |
点评:本题主要考查了单项式,解题的关键是求出单项式的排列规律.

练习册系列答案
相关题目
关于x,y的单项式ax2y,bxy2,
x2y,3xy2的和,合并同类项后结果是-6xy2,则a,b的值分别是( )
| 1 |
| 2 |
A、a=-
| ||
B、a=-
| ||
C、a=
| ||
D、a=
|
 如图所示的正方体沿某些棱展开后,能得到的平面图形是( )
如图所示的正方体沿某些棱展开后,能得到的平面图形是( )A、 |
B、 |
C、 |
D、 |
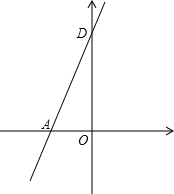 如图,已知直线y=2x+6与x轴、y轴分别交于A、D两点,抛物线y=ax2+bx+2(a≠0)经过点A和点B(1,0).
如图,已知直线y=2x+6与x轴、y轴分别交于A、D两点,抛物线y=ax2+bx+2(a≠0)经过点A和点B(1,0).