题目内容
6.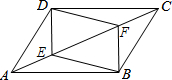 已知:如图所示,?ABCD中,E,F分别是AC上两点,且AE=FC.求证:
已知:如图所示,?ABCD中,E,F分别是AC上两点,且AE=FC.求证:(1)△ADE≌△CBF;
(2)四边形DEBF是平行四边形.
分析 (1)由平行四边形的性质得出AD=BC,AB∥CD,∠DAE=∠BCF,由SAS证明△ADE≌△CBF即可;
(2)连接BD,由平行四边形的性质得出OA=OC,OB=OD,由已知条件得出OE=OF,即可得出结论.
解答 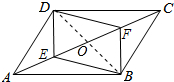 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=CB}&{\;}\\{∠DAE=∠BCF}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△CBF(SAS);
(2)连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形.
点评 本题主要考查了平行四边形的性质、全等三角形的判定及性质;熟练掌握平行四边形的性质,通过作辅助线得出OE=OF是解决(2)的关键.

练习册系列答案
相关题目
3.抛物线y=2x2-8x-6的顶点坐标是( )
| A. | (-2,-14) | B. | (-2,14) | C. | (2,14) | D. | (2,-14) |
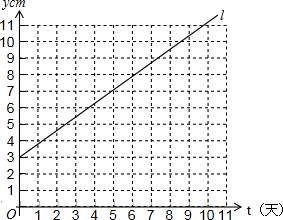 如图,某植物t天后的高度为y cm,l反应了y与t之间的关系.根据图象回答下列问题:
如图,某植物t天后的高度为y cm,l反应了y与t之间的关系.根据图象回答下列问题: