题目内容
2.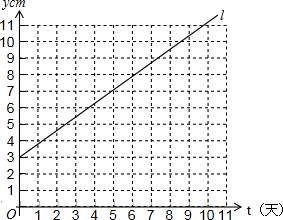 如图,某植物t天后的高度为y cm,l反应了y与t之间的关系.根据图象回答下列问题:
如图,某植物t天后的高度为y cm,l反应了y与t之间的关系.根据图象回答下列问题:(1)3天后该植物高度为多少?
(2)预测该植物12天后的高度;
(3)几天后该植物的高度为10cm?
(4)图象对应的一次函数y=kt+b中,k和b的实际意义分别是什么?
分析 (1)利用待定系数法求出y与t之间的函数关系式,当t=3,求出y的值,即可解答;
(2)当t=12时,代入函数关系式求出y的值,即可解答;
(3)当y=10时,代入函数关系式求出t的值,即可解答;
(4)k表示植株生长率,b表示原先植株高.
解答 解:(1)设y=kt+b,
把(0,3),(6,8)代入y=kt+b得:
$\left\{\begin{array}{l}{0+b=3}\\{6k+b=8}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=\frac{5}{6}}\\{b=3}\end{array}\right.$
∴y=$\frac{5}{6}$t+3,
当t=3时,y=$\frac{5}{6}×3+3=\frac{14}{3}$,
答:3天后该植物高度为$\frac{14}{3}$cm.
(2)当t=12时,y=$\frac{5}{6}×12+3$=13,
答:预测该植物12天后的高度为13cm.
(3)当y=10时,$\frac{5}{6}$t+3=10,
解得:t=8.4,
答:8.4天后该植物的高度为10cm.
(4)k表示植株生长率,b表示原先植株高.
点评 本题考查了一次函数的应用,解决本题的关键是利用待定系数法求一次函数的解析式.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
11.如果关于x的方程(m-2)${x}^{{m}^{2}-2}$-2x-12=0是关于x的一元二次方程,那么m的值为( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 都不对 |
12.下列各式中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=3}\\{z+x=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=5}\\{{y}^{2}=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=4}\\{\frac{1}{x}+\frac{1}{y}=9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+11}\\{2x=y}\end{array}\right.$ |
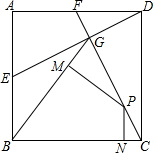 如图,正方形ABCD中,点E是AB的中点,连接DE,在DE上取一点G,连接BG,使BG=BC,连接CG并延长与AD交于点F,在CG上取一动点P(不与点C,点G重合),过点P分别作BG和BC的垂线,垂足分别为点M,点N.若四边形AEGF的面积是$\frac{4}{5}$,则PM+PN的值为$\frac{8}{5}$.
如图,正方形ABCD中,点E是AB的中点,连接DE,在DE上取一点G,连接BG,使BG=BC,连接CG并延长与AD交于点F,在CG上取一动点P(不与点C,点G重合),过点P分别作BG和BC的垂线,垂足分别为点M,点N.若四边形AEGF的面积是$\frac{4}{5}$,则PM+PN的值为$\frac{8}{5}$.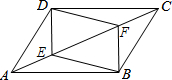 已知:如图所示,?ABCD中,E,F分别是AC上两点,且AE=FC.求证:
已知:如图所示,?ABCD中,E,F分别是AC上两点,且AE=FC.求证: