题目内容
18.将下列分式分别化成最简分式:(1)$\frac{6{m}^{2}{n}^{3}}{3mn}$;(2)$\frac{-20x}{25{x}^{2}}$;
(3)$\frac{9ab}{12{a}^{2}}$;(4)$\frac{2(x+y)^{2}}{x+y}$.
分析 (1)约去公因式3mn即可;
(2)约去公因式5x即可;
(3)约去公因式4a即可;
(4)约去公因式x+y即可.
解答 解:(1)原式=2mn2;
(2)原式=-$\frac{4}{5x}$;
(3)原式=$\frac{3b}{4a}$;
(4)原式=2x+2y.
点评 本题考查了最简分式:一个分式的分子与分母没有公因式时,叫最简分式.本题的关键是找出分子分母的公因式.

练习册系列答案
相关题目
8.若a,b互为相反数,c,d互为倒数,|m|=2,则$\frac{a+b}{{m}^{3}+1}$+m-cd的值为( )
| A. | 4 | B. | -3 | C. | 1 | D. | -3或1 |
13.下列变形属于移项的是( )
| A. | 由-$\frac{1}{4}$x=2,得x=-8 | B. | 由8x+7=3,得8x+7-6=3-6 | ||
| C. | 由8=-5x+2,得5x=2-8 | D. | 由$\frac{11}{6}$=-2a,得-2a=$\frac{11}{6}$ |

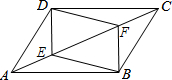 已知:如图所示,?ABCD中,E,F分别是AC上两点,且AE=FC.求证:
已知:如图所示,?ABCD中,E,F分别是AC上两点,且AE=FC.求证: