Question

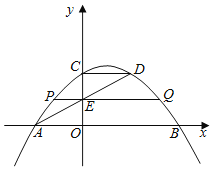
【题目】如图，一次函数的图象与反比例函数的图象交于第二、四象限内的点和点．过点作轴的垂线，垂足为点，的面积为4．

（1）分别求出和的值；

（2）结合图象直接写出的解集；

（3）在轴上取点，使取得最大值时，求出点的坐标．

Answer 1

【答案】（1），；（2）或； （3）

【解析】

（1）根据题意利用三角形面积公式求得，得到，将A代入反比例函数，求出反比例函数解析式，再把B代入解析式，即可解答

（2）根据函数图象结合解析式即可判断

（3）作点关于轴的对称点，直线与轴交于，得到 ，设直线的关系式为，把将 ，代入得到解析式，即可解答

（1）∵点，

∴，

∵，即，

∴，

∵点在第二象限，

∴ ，

将代入得：，

∴反比例函数的关系式为：，

把代入得：，

∴

因此，；

（2）由图象可以看出的解集为：或；

（3）如图，作点关于轴的对称点，直线与轴交于，

此时最大，

∵

∴

设直线的关系式为，将 ，代入得：

解得：，，

∴直线的关系式为，

当时，即，解得，

∴