题目内容
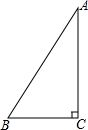
17. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 根据勾股定理,可得BC的长,根据锐角的余弦等于邻边比斜边,可得答案.
解答 解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理,得
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
cosB=$\frac{BC}{AB}$=$\frac{4}{5}$,
故选:B.
点评 本题考查了锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
8.若一个扇形的半径是18cm,且它的弧长是12π cm,则此扇形的圆心角等于( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
9.有这样一个问题:探究函数y=$\frac{1}{x-1}$+x的图象与性质.
小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
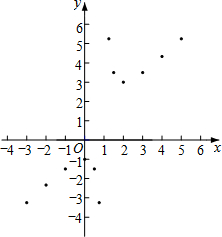
小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{3}{4}$ | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{13}{4}$ | -$\frac{7}{3}$ | -$\frac{3}{2}$ | -1 | -$\frac{3}{2}$ | -$\frac{13}{4}$ | $\frac{21}{4}$ | $\frac{7}{2}$ | 3 | $\frac{7}{2}$ | m | $\frac{21}{4}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
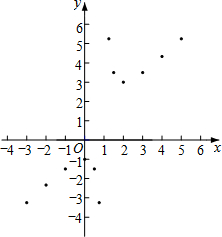
6.下列各数:π,$\frac{4}{3}$,0,-1中,无理数是( )
| A. | π | B. | $\frac{4}{3}$ | C. | 0 | D. | -1 |
7. 要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?
要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?
 要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?
要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?| A. | 2.5m | B. | 5m | C. | 4m | D. | 无法确定 |
 如图:在Rt△ABC中,∠C=90°,BC=8,∠B=60°,解直角三角形.
如图:在Rt△ABC中,∠C=90°,BC=8,∠B=60°,解直角三角形.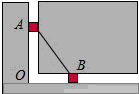 图中的两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米.问:当滑块A向下滑到O点时,滑块B滑动了10厘米.
图中的两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米.问:当滑块A向下滑到O点时,滑块B滑动了10厘米.