题目内容
5．
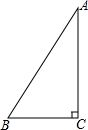如图：在Rt△ABC中，∠C=90°，BC=8，∠B=60°，解直角三角形．
分析 根据三角形的内角和求出∠A，再根据正弦定理求出AB，最后根据勾股定理即可求出AC．
解答 解：∵∠C=90°，∠B=60°，
∴∠A=30°，
∴sinA=$\frac{BC}{AB}$=$\frac{8}{AB}$=$\frac{1}{2}$，
∴AB=16，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{6}^{2}-{8}^{2}}$=8$\sqrt{3}$．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．解直角三角形要用到的关系：锐角直角的关系：∠A+∠B=90°；三边之间的关系：a2+b2=c2；边角之间的关系：锐角三角函数关系．
练习册系列答案
相关题目
15．设a、b是两个整数，若定义一种运算“△”，a△b=a2+ab，则方程x△（x-2）=12的实数根是（ ）
| A． | x1=-2，x2=3 | B． | x1=2，x2=-3 | C． | x1=-1，x2=6 | D． | x1=1，x2=-6 |
16．一次函数y=-2x+1的图象与y轴的交点坐标是（ ）
| A． | （-2，0） | B． | （$\frac{1}{2}$，0） | C． | （0，2） | D． | （0，1） |
20．在Rt△ABC中，∠C=90°，BC=1，那么AB的长为（ ）
| A． | sinA | B． | cosA | C． | $\frac{1}{cosA}$ | D． | $\frac{1}{sinA}$ |
10．已知一次函数y=kx+b的图象经过第一、二、三象限，则b的值可以是（ ）
| A． | 2 | B． | 0 | C． | -1 | D． | -2 |
17．
如图，在Rt△ABC中，∠C=90°，AC=3，AB=5，则cosB的值为（ ）
如图，在Rt△ABC中，∠C=90°，AC=3，AB=5，则cosB的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
14．某圆锥的母线长为6cm，其底面圆半径为3cm，则它的侧面积为（ ）
| A． | 18πcm2 | B． | 18cm2 | C． | 36πcm2 | D． | 36cm2 |
