Question

12．现有一张长为12cm、宽为10cm的矩形纸片，王梦要在该纸片上剪下一个腰长为8cm的等腰三角形，并且使得该等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上，则王梦所剪下的等腰三角形的面积不可能为（　　）

• A． 16$\sqrt{3}$cm²
• B． 8$\sqrt{15}$cm²
• C． 32cm²
• D． 18cm²

Answer 1

分析 因为等腰三角形腰的位置不明确，所以分（1）一腰在矩形的长上，（2）一腰在矩形的宽上，（3）腰长在矩形相邻的两边上，三种情况讨论．（1）先求出AE边上的高DF，再代入面积公式求解即可；（2）先利用勾股定理求出AE边上的高BF，再代入面积公式求解即可；（3）△AEF为等腰直角三角形，直接利用面积公式求解即可．

解答 解：分三种情况计算：
（1）当AE=EF=8厘米时，如图

DF=$\sqrt{{8}^{2}-（12-8）^{2}}$=4$\sqrt{3}$厘米，
∴S_△AEF=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×8×4$\sqrt{3}$=16$\sqrt{3}$厘米²，故A可能；
（2）当AE=EF=8厘米时，如图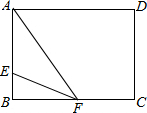

BF=$\sqrt{{8}^{2}-（10-8）^{2}}$=2$\sqrt{15}$厘米，
∴S_△AEF=$\frac{1}{2}$•AE•BF=$\frac{1}{2}$×8×2$\sqrt{15}$=8$\sqrt{15}$厘米²，故B可能；
（3）当AE=AF=8厘米时，

∴S_△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$×8×8=32厘米²，故C可能．
不可能的是选项D．
故选D．

点评 本题主要考查矩形的角是直角的性质和勾股定理的运用，要根据三角形的腰长的不确定分情况讨论是解题的关键也是此题的难点．