题目内容
20.解下列不等式组:(1)$\left\{\begin{array}{l}{3x+1≥3}\\{\frac{x}{4}<x-1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{5x-6≤2(x+3)}\\{\frac{x}{4}-1<\frac{x-3}{3}}\end{array}\right.$.
分析 (1)分别求出每一个不等式的解集,根据口诀:同大取大确定不等式组的解集;
(2)分别求出每一个不等式的解集,根据口诀:大小小大中间找确定不等式组的解集.
解答 解:(1)解不等式3x+1≥3,得:x≥$\frac{2}{3}$,
解不等式$\frac{x}{4}$<x-1,得:x>$\frac{4}{3}$,
故不等式组的解集为:x>$\frac{4}{3}$;
(2)解不等式5x-6≤2(x+3),得:x≤4,
解不等式$\frac{x}{4}$-1<$\frac{x-3}{3}$,得:x>0,
故不等式组的解集为:0<x≤4.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.三角形的两条边长分别为7和3,则第三边的长可以为( )
| A. | 3cm | B. | 10cm | C. | 4cm | D. | 7cm |
12.以下微信图标不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9. 如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )
如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )
 如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )
如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
10.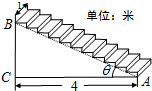 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )| A. | $\frac{4}{sinθ}$米2 | B. | $\frac{4}{cosθ}$米2 | C. | (4+$\frac{4}{tanθ}$)米2 | D. | (4+4tanθ)米2 |
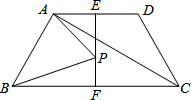 如图,在四边形ABCD中,AD∥BC,AB=CD且AB与CD不平行,AD=2,∠BCD=60°,对角线CA平分∠BCD,E,F分别是底边AD,BC的中点,连接EF,点P是EF上的任意一点,连接PA,PB,则PA+PB的最小值为2$\sqrt{3}$.
如图,在四边形ABCD中,AD∥BC,AB=CD且AB与CD不平行,AD=2,∠BCD=60°,对角线CA平分∠BCD,E,F分别是底边AD,BC的中点,连接EF,点P是EF上的任意一点,连接PA,PB,则PA+PB的最小值为2$\sqrt{3}$.