题目内容
9. 如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )
如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
分析 根据题意平移AB使A点与P点重合,进而得出,△QPB′是直角三角形,再利用tan∠QMB=tan∠P=$\frac{QB′}{PB′}$,进而求出答案.
解答 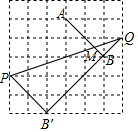 解:如图所示:平移AB使A点与P点重合,连接B′Q,
解:如图所示:平移AB使A点与P点重合,连接B′Q,
可得∠QMB=∠P,
∵PB′=2$\sqrt{2}$,PQ=2$\sqrt{10}$,B′Q=4$\sqrt{2}$,
∴PB′2+QB′2=PQ2,
∴△QPB′是直角三角形,
∴tan∠QMB=tan∠P=$\frac{QB′}{PB′}$=$\frac{4\sqrt{2}}{2\sqrt{2}}$=2.
故选:D.
点评 此题主要考查了勾股定理以及锐角三角函数关系,正确得出△QPB′是直角三角形是解题关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
4.计算|-8|-(-$\frac{1}{2}$)0的值是( )
| A. | -7 | B. | 7 | C. | 7$\frac{1}{2}$ | D. | 9 |
1. 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
19.-12等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
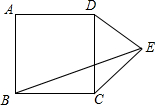 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=$\frac{1}{3}$.
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=$\frac{1}{3}$.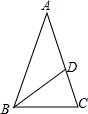 如图,在△ABC中,AB=AC=1,BC=$\frac{\sqrt{5}-1}{2}$,在AC边上截取AD=BC,连接BD.
如图,在△ABC中,AB=AC=1,BC=$\frac{\sqrt{5}-1}{2}$,在AC边上截取AD=BC,连接BD.