题目内容
10.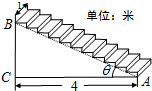 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )| A. | $\frac{4}{sinθ}$米2 | B. | $\frac{4}{cosθ}$米2 | C. | (4+$\frac{4}{tanθ}$)米2 | D. | (4+4tanθ)米2 |
分析 由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.
解答 解:在Rt△ABC中,BC=AC•tanθ=4tanθ(米),
∴AC+BC=4+4tanθ(米),
∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米2);
故选:D.
点评 本题考查了解直角三角形的应用、矩形面积的计算;由三角函数表示出BC是解决问题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
1. 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5. 如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
 如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )| A. | Φ45.02 | B. | Φ44.9 | C. | Φ44.98 | D. | Φ45.01 |
2.下列计算正确的是( )
| A. | a3+a3=a6 | B. | 3a-a=3 | C. | (a3)2=a5 | D. | a•a2=a3 |
19.-12等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
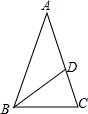 如图,在△ABC中,AB=AC=1,BC=$\frac{\sqrt{5}-1}{2}$,在AC边上截取AD=BC,连接BD.
如图,在△ABC中,AB=AC=1,BC=$\frac{\sqrt{5}-1}{2}$,在AC边上截取AD=BC,连接BD.