题目内容
15.已知底面积为4π的圆锥侧面展开图为一个半径为2的扇形,则这个圆锥的侧面积为4π.分析 先根据圆锥的表面积为4π求出底面半径r=2,再由圆锥的母线长l=2,利用圆锥的侧面积S侧=πrl,代入计算即可.
解答 解:∵底面积为4π的圆锥侧面展开图为一个半径为2的扇形,
∴πr2=4π,l=2,
∴r=2,
∴这个圆锥的侧面积为S侧=πrl=π×2×2=4π.
故答案为4π.
点评 本题考查了圆锥的计算,用到的知识点:圆锥的侧面积:S侧=πrl;圆锥的母线与展开后所得扇形的半径相等.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | x6•x2=x12 | B. | x2+x2=2x2 | C. | (x2)3=x5 | D. | x6÷x2=x3 |
10.已知反比例函数的图象经过点(1,-8),则它的图象一定也经过( )
| A. | (-2,-4) | B. | (-2,4) | C. | (-1,-8) | D. | (1,8) |
20. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}\sqrt{2}$ | D. | 2 |
7.下列关于比例线段和相似的叙述,不正确的是( )
| A. | 若a:b=c:d,则ac=bd | |
| B. | 相似三角形的面积比等于相似比的平方 | |
| C. | 点C是线段AB的黄金分割点,且AC>BC,则$\frac{BC}{AB}=\frac{{3-\sqrt{5}}}{2}$ | |
| D. | 经过位似多边形对应顶点的直线一定交于同一点 |
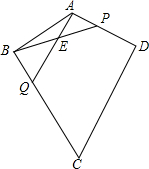 如图,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ和BP交于点E,且∠BEQ=90°-$\frac{1}{2}$∠BAD,设A、P两点的距离为x.
如图,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ和BP交于点E,且∠BEQ=90°-$\frac{1}{2}$∠BAD,设A、P两点的距离为x.