题目内容
5.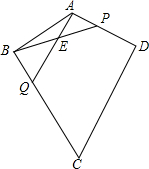 如图,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ和BP交于点E,且∠BEQ=90°-$\frac{1}{2}$∠BAD,设A、P两点的距离为x.
如图,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ和BP交于点E,且∠BEQ=90°-$\frac{1}{2}$∠BAD,设A、P两点的距离为x.(1)求∠BEQ的正切值;
(2)设$\frac{AE}{PE}$=y,求y关于x的函数解析式及定义域;
(3)当△AEP是等腰三角形时,求B、Q两点的距离.
分析 (1)求∠BEQ的正切值,要把∠BEQ放在直角三角形中进行解决,根据AB=AD=5,CB=CD=8可知,连接四边形ABCD的对角线可得到AC⊥BD,可通过∠BEQ=90°-$\frac{1}{2}$∠BAD和∠ABD=90°-$\frac{1}{2}$∠BAD,可知∠BEQ=∠ABD,通过求∠ABD的正切值来求得∠BEQ的正切值.
(2)设AQ与BD交于点F,由(1)中的∠BEQ=∠ABD,AB=AD,CB=CD,得到∠AEP=∠ADF,从而可得△FAB∽△PBD,△APE∽△AFD.先由△FAB∽△PBD中的比例式$\frac{BF}{PD}$=$\frac{AB}{BD}$用含x的式子表示BF=$\frac{5}{8}$(5-x),DF=BD-BF=$\frac{39+5x}{8}$,再用△APE∽△AFD中的比例式$\frac{AE}{PE}$=$\frac{AD}{DF}$用含x的式子表示y=$\frac{40}{39+5x}$(因为点P是在线段AD上移动,所以x的取值范围是0<x<5).
(3)由于题中没有说明△AEP中那两条边相等,所以要分情况讨论:①当AE=PE时,y=$\frac{40}{39+5x}$=1 可得 x=$\frac{1}{5}$,可求出OF=1,作QH⊥BD,构造相似三角形,Rt△QHF∽Rt△AOF设BQ=a,用含有a的式子表示BH=$\frac{1}{2}$a,QH=$\frac{\sqrt{3}}{2}$a,根据$\frac{FH}{HQ}$=$\frac{OF}{OA}$=$\frac{1}{3}$,可解得BQ=a=9-3$\sqrt{3}$;②当AP=PE时,易证△PAE∽△ABD,根据$\frac{AE}{PE}$=$\frac{BD}{AD}$=$\frac{8}{5}$,可得x=-$\frac{14}{5}$,因为不合题意,故此种情况舍去;③当AP=AE时,易证△AEP∽△ABD,利用$\frac{AE}{PE}$=$\frac{AB}{BD}$=$\frac{5}{8}$,可得AP=5,此时B、Q重合,即BQ=0(舍去).综合这三种情况可以求得B、Q两点间距离为9-3$\sqrt{3}$.
解答 解:
(1)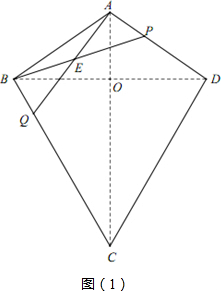
连接BD、AC,交点于点O,(图1)
∵AB=AD=5,CB=CD=8
∴AC⊥BD,且OB=OD=$\frac{1}{2}$BD=4
∴∠ABD=90°-∠BAC=90°-$\frac{1}{2}$∠BAD
∴∠BEQ=∠ABD
在Rt△ABO中,AB=5,OB=4
∴tan∠BEQ=tan∠ABO=$\frac{AO}{BO}$=$\frac{3}{4}$
(2)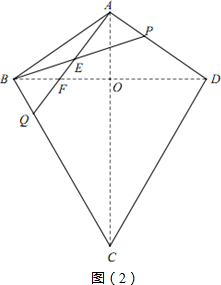
设AQ与BD交于点F(图2)
∵∠BEQ=∠ABD=∠AEP∠AFB=∠BFE
∴△FBE∽△FAB,△FBE∽△PBD
∴△FAB∽△PBD
$\frac{BF}{PD}$=$\frac{AB}{BD}$,即$\frac{BF}{5-x}$=$\frac{5}{8}$
∴BF=$\frac{5}{8}$(5-x),DF=BD-BF=$\frac{39+5x}{8}$
又∵∠BEQ=∠ABD=∠AEP=∠ADB∠EAP=∠DAF
∴△APE∽△AFD
∴y=$\frac{AE}{PE}$=$\frac{AD}{DF}$=$\frac{5}{\frac{39+5x}{8}}$
整理得:y=$\frac{40}{39+5x}$(0<x<5)
(3)如图3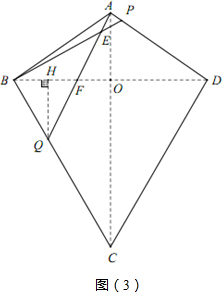
①当AE=PE时,y=$\frac{40}{39+5x}$=1
解得 x=$\frac{1}{5}$
∵y=$\frac{AE}{PE}$=$\frac{AD}{DF}$=$\frac{40}{39+5x}$
∴DF=$\frac{39+5x}{8}$=5
∴OF=DF-OD=5-4=1
作QH⊥BD,
∵AO⊥BD,∠ACB=30°
∴∠BQH=30°,Rt△QHF∽Rt△AOF
设BQ=a,则BH=$\frac{1}{2}$a,QH=$\frac{\sqrt{3}}{2}$a,则
$\frac{FH}{HQ}$=$\frac{OF}{OA}$=$\frac{1}{3}$,即$\frac{3-\frac{1}{2}a}{\frac{\sqrt{3}}{2}a}$=$\frac{1}{3}$,解得BQ=a=9-3$\sqrt{3}$;
②当AP=PE时,∠PAE=∠PEA
∵∠AEP=∠BEQ=∠ABD=∠ADB
∴△PAE∽△ABD
又∵BD=BC=CD=8
∴$\frac{AE}{PE}$=$\frac{BD}{AD}$=$\frac{8}{5}$,即$\frac{40}{39+5x}$=$\frac{8}{5}$,
解得x=-$\frac{14}{5}$(不合题意,舍去)
③当AP=AE时,∠AEP=∠APE=∠ABD=∠ADB
∴△AEP∽△ABD
∴$\frac{AE}{PE}$=$\frac{AB}{BD}$=$\frac{5}{8}$,即$\frac{40}{39+5x}$=$\frac{5}{8}$,解得x=5,即AP=5
此时B、Q重合,即BQ=0(舍去).
综上可知,B、Q两点间距离为9-3$\sqrt{3}$.
点评 本题考查的知识点有:①通过等量代换的方法把一个角放到直角三角形中求三角函数值的方法;②利用相似三角形的相似比作为等量关系,用含x的式子表示某条线段或线段比;③利用△AEP是等腰三角形,求B、Q两点的距离时,没有说清那两条边相等的情况下要分三种情况考虑问题,然后再根据相等的角或边找到对应的等量关系求x的值.

| A. | y=2(x+1)2+3 | B. | y=2(x+1)2-3 | C. | y=2(x-1)2-3 | D. | y=2(x-1)2+3 |
 如图,A,B,C这三个点表示三个工厂,它们在同一个圆上,要建立一个供水站,使它到这三个工厂的距离相等,请找出供水站的位置.
如图,A,B,C这三个点表示三个工厂,它们在同一个圆上,要建立一个供水站,使它到这三个工厂的距离相等,请找出供水站的位置. 如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.
如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.
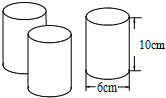 小华家来了两位客人,妈妈冲了900mL的果汁,如果用图中三个大小完全相同的玻璃杯装果汁,这些果汁能将这三个杯子装满吗?请说明理由.(π取3.14)
小华家来了两位客人,妈妈冲了900mL的果汁,如果用图中三个大小完全相同的玻璃杯装果汁,这些果汁能将这三个杯子装满吗?请说明理由.(π取3.14)