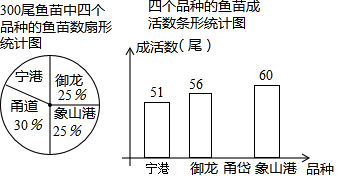
题目内容
6．已知点A（1，5），B（4，2），点P在x轴上，当PA-PB最大时，点P的坐标为（6，0）．分析 于三角形三边关系可得PA-PB≤AB，当A、B、P共线时，PA-PB的值最大．求出直线AB的解析式，再求出直线AB与x轴的交点即可解决问题．
解答 解：
如图PA-PB≤AB，当A、B、P共线时，PA-PB的值最大．
∵A（1，5），B（4，2），
∴直线AB的解析式为y=-x+6，可得P′（6，0），
∴当P点坐标为（6，0）时，PA-PB的值最大、
故答案为（6，0）．
点评 本题考查轴对称-最短问题、坐标与图形的性质、一次函数的性质、三角形的三边关系等知识，解题的关键是灵活应用三角形的三边关系解决最值问题，属于中考常考题型．
练习册系列答案
口算能手系列答案
相关题目
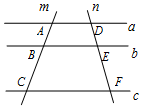如图，已知直线a∥b∥c，直线m交直线a，b，c于点A，B，C，直线n交直线a，b，c于点D，E，F，若$\frac{AB}{BC}=\frac{1}{2}$，则$\frac{DE}{DF}$=$\frac{1}{3}$．
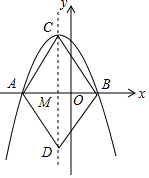如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（-2，0），B（1，0），顶点为C，对称轴于x轴交于点M，连接AC，BC，作AD∥BC交对称轴于点D，连接BD，有下列5个结论：①a-b=0；②当-2＜x＜1时，y＞0；③四边形ADBC是菱形；④9a-3b+c＞0；⑤c=2a，其中正确的个数是（ ）
1．4个红球、6个白球放入一个不透明的盒子里，从中任摸出5个球，恰好红球、白球都摸到，这个事件是（ ）
| A． | 必然事件 | B． | 不可能发生 | C． | 可能发生 | D． | 很可能发生 |
如图，抛物线y1=$\frac{1}{2}$（x+1）2+1与y2=a（x-4）2-3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：