题目内容
4. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )| A. | 1.8 | B. | 2.4 | C. | 3.2 | D. | 3.6 |
分析 连接BF,根据三角形的面积公式求出BH,得到BF,根据直角三角形的判定得到∠BFC=90°,根据勾股定理求出答案.
解答 解:连接BF,
∵BC=6,点E为BC的中点,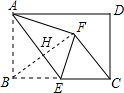
∴BE=3,
又∵AB=4,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5,
∴BH=$\frac{12}{5}$,
则BF=$\frac{24}{5}$,
∵FE=BE=EC,
∴∠BFC=90°,
∴CF=$\sqrt{{6}^{2}-(\frac{24}{5})^{2}}$=3.6.
故选:D.
点评 本题考查的是翻折变换的性质和矩形的性质,掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
9.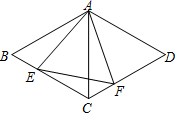 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )| A. | $4\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |





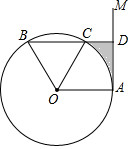 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.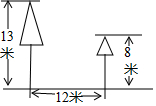 如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞13米.
如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞13米.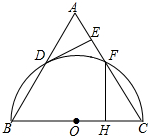 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.