题目内容
3.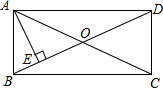 已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )
已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )| A. | 22.5° | B. | 30° | C. | 45° | D. | 35° |
分析 由矩形的性质得出∠BAD=90°,OA=OD,得出∠OAD=∠ODA,再求出∠DAE=67.5°,∠OAD=22.5°,即可求出∠EAC.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OD,
∴∠OAD=∠ODA,
∵∠DAE:∠BAE=3:1,
∴∠DAE=$\frac{3}{4}$×90°=67.5°,
∵AE⊥BD,
∴∠AED=90°,
∴∠OAD=+ODA=22.5°,
∴∠EAC=67.5°-22.5°=45°.
故选:C.
点评 本题考查了矩形的性质、等腰三角形的性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
13.如果把分式$\frac{3n}{{{m^2}-{n^2}}}$中的m和n都扩大3倍,那么分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
13.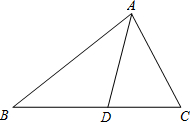 在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
 在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )| A. | 25° | B. | 35° | C. | 37.5° | D. | 45° |
 如图所示,正方形ABCD的对角线AC、BD相交于点O,DE平分∠ODC交OC于点E,若AB=1,则线段CE的长为$\sqrt{2}-1$.
如图所示,正方形ABCD的对角线AC、BD相交于点O,DE平分∠ODC交OC于点E,若AB=1,则线段CE的长为$\sqrt{2}-1$.