题目内容
12.如图1,等腰直角三角形ABC和等腰直角三角形CEF,∠ABC=∠CEF=90°,点C,B,E在同一条直线上,M是AF的中点.(1)求证:MB∥CF;
(2)将△CEF绕顶点C顺时针旋转,使点E落在射线AB上,如图2,猜想BM与EM的数量关系和位置关系,并说明理由.

分析 (1)延长AB交CF于点D,证明BM为△ADF的中位线即可;
(2)取AC,CF的中点P,Q,连接BP,EQ,MQ,PM,设PN交EQ于点N,由M是AF的中点,得到PM是△ACF的中位线,推出四边形CQMP是平行四边形,得到BP=PC=MQ,PM=CQ=QE,∠3=∠4,证得△BPM≌△EMQ,得出BM=ME,BMP=∠MEQ,由于EQ⊥CF,PM∥CF求出EQ⊥PM,得到∠MNE=90°由等量代换得出∠PMB+∠5=90°,于是得出答案BM⊥EM.
解答 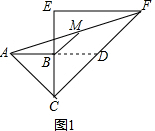 解:(1)如图1,延长AB交CF于点D,
解:(1)如图1,延长AB交CF于点D,
∵△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD,
∴点B为线段AD的中点,
又∵点M为线段AF的中点,
∴BM为△ADF的中位线,
∴BM∥CF;
(2)BM=EM,BM⊥EM,
如图2,取AC,CF的中点P,Q,连接BP,EQ,MQ,PM,
设PN交EQ于点N,
∵M是AF的中点,
∴PM∥CF,PM=$\frac{1}{2}$CF=CQ,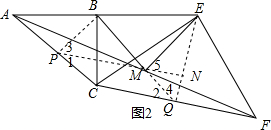
∴四边形CQMP是平行四边形,
∴BP=PC=MQ,PM=CQ=QE,∠1=∠2,
∴∠3=∠4,
在△PBM与△EMQ中$\left\{\begin{array}{l}{PB=MQ}\\{∠3=∠4}\\{PM=QE}\end{array}\right.$,
∴△BPM≌△EMQ,
∴BM=ME,∠BMP=∠MEQ,
∵EQ⊥CF,PM∥CF,
∴EQ⊥PM,
∴∠MNE=90°,
∴∠MEQ+∠5=90°,
∴PMB+∠5=90°,
∴BM⊥EM.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,三角形的中位线的性质,平行四边形的判定和性质,准确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.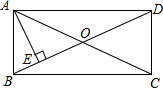 已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )
已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )
 已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )
已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )| A. | 22.5° | B. | 30° | C. | 45° | D. | 35° |
20.将抛物线y=4x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是( )
| A. | y=4(x+2)2-3 | B. | y=4(x-2)2-3 | C. | y=4(x+2)2+3 | D. | y=4(x+3)2+2 |
17.方程x$\sqrt{2-x}$=$\sqrt{2-x}$的解是( )
| A. | x1=2,x1=1,x3=-1 | B. | x1=2,x2=1 | C. | x1=2,x2=-1 | D. | x1=1,x2=-1 |
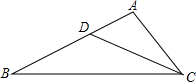 如图所示,点D是△ABC的AB边上一点,且AD=1,BD=2,AC=$\sqrt{3}$.求证:△ACD∽△ABC.
如图所示,点D是△ABC的AB边上一点,且AD=1,BD=2,AC=$\sqrt{3}$.求证:△ACD∽△ABC.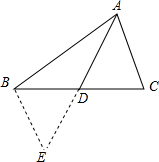 如图,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.
如图,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.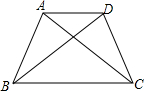 如图,已知AB=CD,AC=BD,说明AD∥BC.
如图,已知AB=CD,AC=BD,说明AD∥BC.