题目内容
18.在平面直角坐标系xOy中,抛物线y=mx2-nx+m-$\frac{5}{4}$关于y轴对称,且经过点(-1,-$\frac{3}{4}$)(1)求m,n的值;
(2)直线l经过点(0,-2)且与y轴垂直,点P是抛物线上一动点,记P到直线l的距离为d,试探索d与线段OP长度的数量关系,并证明;
(3)若A(1,1),点P是抛物线上一动点,请结合函数图象,直接写出OP+AP的最小值,以及取得最小值时点P的坐标.
分析 (1)利用抛物线的对称性和过已知点,可求得m、n的值;
(2)可设出P点坐标,再用P点坐标分别表示出d和OP的长,可得出d=OP;
(3)根据(2)的结论,可知OP的长与P到直线l的距离相等,可过A作直线垂直于x轴,与抛物线的交点即为满足条件的P点,容易求得OP+AP和P点坐标.
解答 解:(1)∵抛物线关于y轴对称,
∴n=0,
∵抛物线经过点(-1,-$\frac{3}{4}$),
∴m+m-$\frac{5}{4}$=-$\frac{3}{4}$,解得m=$\frac{1}{4}$;
(2)d=OP.证明如下:
由(1)可知抛物线解析式为y=$\frac{1}{4}$x2-1,故可设P点坐标为(x,$\frac{1}{4}$x2-1),
∴点P到直线l的距离d=$\frac{1}{4}$x2-1-(-2)=$\frac{1}{4}$x2+1,
又∵OP=$\sqrt{{x}^{2}+(\frac{1}{4}{x}^{2}-1)^{2}}$=$\sqrt{{x}^{2}+\frac{1}{16}{x}^{4}-\frac{1}{2}{x}^{2}+1}$=$\sqrt{\frac{1}{16}{x}^{4}+\frac{1}{2}{x}^{2}+1}$=$\sqrt{(\frac{1}{4}{x}^{2}+1)^{2}}$=$\frac{1}{4}$x2+1,
∴d=OP;
(3)如图,过A作直线t⊥x轴,与抛物线交于点P,交直线l于点B,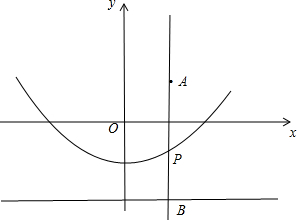
由(2)可知PO=PB,
∴OP+AP=PB+AP=AB,
∴此时P点满足条件,
∴OP+AP=1-(-2)=3,把x=1代入抛物线解析式可求得y=-$\frac{3}{4}$,
∴OP+AP的最小值为3,此时点P的坐标为(1,-$\frac{3}{4}$).
点评 本题主要考查二次函数的综合应用,涉及待定系数法、二次函数的性质、勾股定理等知识点.在(1)中确定出n是解题的关键,在(2)中利用勾股定理表示出OP的距离是解题的关键,在(3)中确定出P点的位置是解题的关键.本题所考查知识相对基础,难度不大.

| A. | 0.1-2=0.01 | B. | ($\frac{1}{2}$)-3=-8 | C. | (-2)-2=4 | D. | (mn-2)-1=$\frac{{n}^{2}}{m}$ |
| A. | 1:2:3:4 | B. | 1:2:2:1 | C. | 2:2:1:1 | D. | 2:1:2:1 |
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{{2^2}+{3^2}}=2+3$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{3}•\sqrt{2}=\sqrt{6}$ |
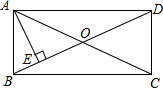 已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )
已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE:∠BAE=3:1,则∠EAC为( )| A. | 22.5° | B. | 30° | C. | 45° | D. | 35° |
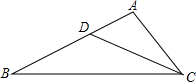 如图所示,点D是△ABC的AB边上一点,且AD=1,BD=2,AC=$\sqrt{3}$.求证:△ACD∽△ABC.
如图所示,点D是△ABC的AB边上一点,且AD=1,BD=2,AC=$\sqrt{3}$.求证:△ACD∽△ABC.