题目内容
8. 在矩形ABCD中,E、F、M分别为AB、BC、CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为5$\sqrt{2}$.
在矩形ABCD中,E、F、M分别为AB、BC、CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为5$\sqrt{2}$.
分析 由四边形ABCD是矩形,得到∠B=∠C=90°,CD=AB=6,根据AE=3,DM=2,于是得到BE=3,CM=4,推出△BEF∽△CFM,得到关于BF的比例式,进而可求出EM,EF的长,再利用勾股定理即可求出EM的长.或过M作MN⊥AB于N,易知MN=7,EN=1,EM=$\sqrt{{1}^{2}+{7}^{2}}$=5$\sqrt{2}$.
解答 解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=6,
∵AE=3,DM=2,
∴BE=3,CM=4,
∵EF⊥FM,
∴∠BEF+∠BFE=∠BFE+∠MFC=90°,
∴∠BEF=∠CFM,
∴△BEF∽△CFM,
∴$\frac{BF}{CM}=\frac{BF}{4}$,
∴$\frac{BF}{4}=\frac{3}{7-BF}$,
解得:BF=3,或BF=4,
∴CF=4,或CF=3,
∴EF=$\sqrt{{3}^{2}+{4}^{2}}$=5,FM=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴EM=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
故答案为:5$\sqrt{2}$.
或过M作MN⊥AB于N,易知MN=7,EN=1,
EM=$\sqrt{{1}^{2}+{7}^{2}}$=5$\sqrt{2}$.
点评 本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
18.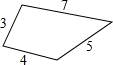 如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
 如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )| A. | 7 | B. | 9 | C. | 10 | D. | 12 |
13.某学校组织了一次知识竞赛,初二年级、初三年级各10名选手的比赛成绩如下(本次竞赛满分10分):
(1)初二成绩的中位数是9.5分,初三成绩的众数是10分;
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
| 初二 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 初三 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
17. 将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )
将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )
 将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )
将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |
 如图是将正方体切去一个角后的几何体,则该几何体的左视图是( )
如图是将正方体切去一个角后的几何体,则该几何体的左视图是( )



 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m与n的关系式可以表示为m=n2+n+2.
填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m与n的关系式可以表示为m=n2+n+2. 如图,已知在矩形ABCD中,AB=6,AD=12,将△ADE沿直线DE对折,使点A落在BC上的点F,则∠ADE=15°,BF=12-6$\sqrt{3}$.
如图,已知在矩形ABCD中,AB=6,AD=12,将△ADE沿直线DE对折,使点A落在BC上的点F,则∠ADE=15°,BF=12-6$\sqrt{3}$.