题目内容
1.省实验中学为了响应国家环境治理的口号,决定抽取七年级和八年级学生代表共30人在校园里植树,已知七年级同学每人每小时可植树2棵,八年级同学每人每小时可植树3棵,学校计划植树3小时.(1)若学校计划3小时内植树不得少于200棵,则七年级同学最多抽取多少人?
(2)若九年级同学不怕延误学习也主动参加了植树活动,每人每小时可植树4棵,九年级派出的同学与八年级同学人数之和是20人,并且八年级同学植树总量大于七年级同学植树总量的1.5倍,九年级同学植树总量小于七年级同学植树总量的3倍,那么如何安排人数可使这次植树的树木最多?
分析 (1)设七年级同学抽取x人,则抽取八年级学生(30-x)人,根据“学校计划3小时内植树不得少于100棵”列出不等式并解答.
(2)设参加植树的八年级学生为y人,则七年级学生为(30-y)人,九年级学生为(20-y)人,根据“八年级同学植树总量大于七年级同学植树总量的1.5倍,九年级同学植树总量小于七年级同学植树总量的3倍”列出不等式组并解答.
解答 解:(1)设七年级同学抽取x人,则抽取八年级学生(30-x)人,依题意得
3×2x+3×3(30-x)≥200,
解得 x≤$\frac{70}{3}$.
∵x是正整数,即x最大值=23.
答:若学校计划3小时内植树不得少于200棵,则七年级同学最多抽取23人;
(2)设参加植树的八年级学生为y人,
依题意得 $\left\{\begin{array}{l}{3y>2(30-y)×1.5}\\{4(20-y)<2(30-y)×3}\end{array}\right.$,
解得 15<y<35.
又∵0<y<20,
∴15<y<20.
∵y是正整数,
∴y可以取16,17,18,19.
∴30-y=14,13,12,11.
20-y=4,3,2,1.
方案一:七年级14人、八年级16人、九年级4人,共植树14×2+16×3+4×4=92(棵).
方案二:七年级13人、八年级17人、九年级3人,共植树13×2+17×3+3×4=89(棵).
方案三:七年级12人、八年级18人、九年级2人,共植树12×2+18×3+2×4=86(棵).
方案四:七年级11人、八年级19人、九年级1人,共植树11×2+19×3+1×4=83(棵).
则方案一可使这次植树的树木最多.
点评 本题考查了一元一次不等式组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案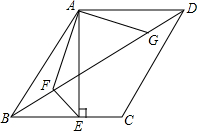 如图,在?ABCD中,AE⊥BC于点E,AE=AD,点F、G是对角线BD上的两点,且△AFG是等腰三角形,∠FAG=90°,若AF=3$\sqrt{2}$,EF=2,则?ABCD的面积为34.
如图,在?ABCD中,AE⊥BC于点E,AE=AD,点F、G是对角线BD上的两点,且△AFG是等腰三角形,∠FAG=90°,若AF=3$\sqrt{2}$,EF=2,则?ABCD的面积为34.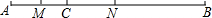 如图,线段AB=9cm,BC=6cm,点M是AC的中点.
如图,线段AB=9cm,BC=6cm,点M是AC的中点.
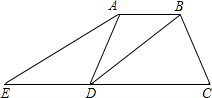 如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.